ECS122A-Cheatsheet

Midterm 1:

---

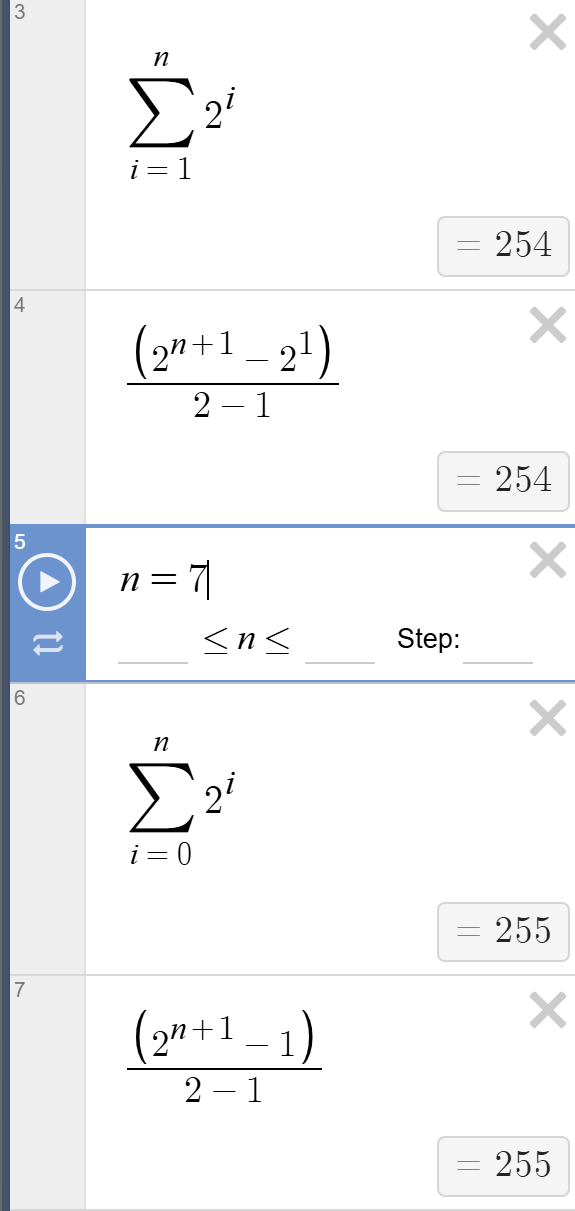
Summation:

Algorithm Approaches

Divide and Conquer:

Divide - The problem into subproblems that are smaller instances of the same problem
Conquer - Solve the smallest instances recursively (calling the same function)

• If instance is small enough, solve directly (base case)
  Combine - Combine the solution to smaller instances into a final answer

Recursion?

3 Methods of Solving Recurrence

Recursive - A function that calls itself
You can tell which will be the biggest contributor via Master Theorem, or inspection

Methods:

1. Recurrence Tree Method (Relevant Lecture)
   1. Find the work done at each level
   2. Find the depth / number of levels
   3. Do a sigma sum, and calculate the work done
   4. You now have work done
      T(n) = 2T(n/2) + O(1)
      Work: (2)
      Depth:
      Total Work:
2. Substitution
   1. Make a guess about the runtime
   2. Prove that it holds true for your guess, if not make a new guess
      T(n) = T(n/6) + T(2n/6) + O(n)
      Guess that T(n) = O(n)
      This would mean that
      T(k) = T(k/6) + T(2k/6) + O(k)
      by IH we can say that this is less than or equal to:
      = c(k/6) + c(2k/6) + ak ck
      c/2 + a c
      a c/2
      2a c
      Our guess holds true, as c can be set to 2a and be true.
3. Master Theorem
   https://www.youtube.com/watch?v=2y0HQGd1-nA
   
   3 Cases:
4. : The tree/subproblems win
   • Solution is
5. : They are both even
   • Solution is
6. : The initial work wins
   • Solution is

Big __

Big-O: An upper bound as n goes to infinity. Saying that for some

Big-: Big O but for lower bound. Saying that for some

Big-: A function is big theta iff T(n) is Big O and Big Omega of some f(n)
Formally:

Proving Big __

For Big O and Big Omega:

Can do the same but proving less than or equal to to prove big Omega

For Big Theta:
Prove that a function is BOTH big O and big Omega of some function. The constants do not need to be the same, just show that the function T(n) is and

Limit lemma:

If

3 Cases:

L=0 => f(n) = O(g(n))
L= => f(n) = (g(n))
L= some C => f(n)=(g(n))

Big-O of Operations:

Merge sort: