Problem 1
a)
Transclude of ECS122A-HW5-2024-12-05-21.51.39.excalidraw
b)
Run BFS from A and fill out the distance array d:
Problem 2
1)
| 0 | 0 | |
| 7 | 2 | 0 |
| 5 | 3 | 7 |
| 2 | 4 | 5 |
| 4 | 5 | 0 |
| 1 | 6 | 4 |
| 8 | 6 | 7 |
| 3 | 6 | 2 |
| 9 | 6 | 5 |
| 6 | 7 | 9 |
| 10 | 10 | 6 |
2)
Transclude of ECS122A-HW5-2024-12-05-22.39.58.excalidraw
Topological Sort:
Problem 3
Find the shortest path tree from every node to node 1 for the graph of Fig.1 using the Bellman-Ford and Dijkstra algorithms. Describe the algorithmic change necessary to answer this question.
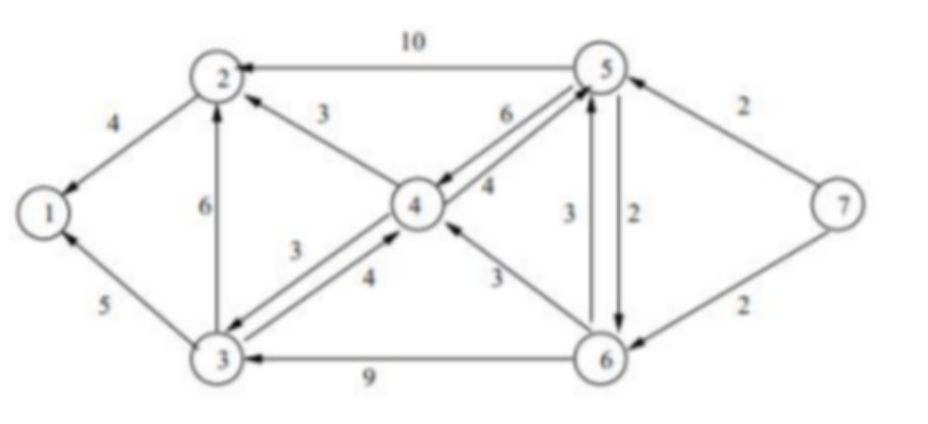
- The first step to run this algorithm is to reverse all of the edges, and find the shortest path from 1 to every other node
- Since the graph has purely positive weights, the resulting shortest path tree will be identical for both Bellman-Ford and Djisktra
| Distance | Path | |
|---|---|---|
| 1 | 0 | 1 |
| 2 | 4 | 2->1 |
| 3 | 5 | 3->1 |
| 4 | 7 | 4->2->1 |
| 5 | 12 | 5->6->4->2->1 |
| 6 | 10 | 6->4->2->1 |
| 7 | 12 | 7->6->4->2->1 |
Transclude of ECS122A-HW5-2024-12-05-23.36.32.excalidraw
- Resulting tree visualized