📗 -> 05/29/25: ECS170-D9

Lecture Slide Link

🎤 Vocab

❗ Unit and Larger Context

Doing Course Review Part 1

✒️ -> Scratch Notes

Seven Properties of Task Environments

States observability
How many agents
Successor states determinism
Agent decisions, episodic or sequential
Environment, static or dynamic
State of the environment and actions, discrete or continuous
Environment, known or unknown
Observable
Agents
Deterministic
Episodic
Static
Discrete

Five Agent Programs

Agent Program - maps from percepts to actions

Simple reflex agent
Model-based reflex agent
Goal-based reflex agent
Utility-based agent
Learning-based agent

Graph Algorithms

b (branching facts) - max num successor nodes
d (depth) - number actions in optimal solution
m (maximum depth) - maximum actions on any path

BFS

BFS is complete
BFS is optimal ~

If all actions have the same cost
Otherwise, its a different problem (road map navigation problem)

Time:
Space:

Every node until depth has to kept in memory and visited, time = space

Intractable with large state space

Uniform Cost Search (UCS)

Also known as: best first search

Instead of expanding the shallowest node, expand the lowest cost node
Implementation similar to BFS, but with a path cost function f to each step

Orders frontier by f
First node on frontier is the one with current lowest path cost

UCS is complete
UCS is optimal

For ANY cost function, will expand cheapest route first

An upgraded BFS, ordering by cost

Iterative Deepening Search

Problems with DFS:

Fails in infinite search spaces
Inefficient if m >> d (m=maximum depth, d=depth of solution)

Idea #1 (Depth Limited Search): Set a limit on search depth

Prevents infinite growth of early paths that do not contain goal node
Succeeds if , fails otherwise

Idea #2 (Iterative Deepening Search, or Iterative Deepening DFS)

Set an initial limit
At each next depth with not goal, increase

Relaxed Problems and Heuristics

The solution to a relaxed problem is a heuristic for the original problem

Example:

For the 8-puzzle, we relax the rules so that a tile can move to any adjacent square (including occuped)
We use the heuristic of total manhattan distance
Since this is a solution to the relaxed problem, it’s a valid heuristic for the original problem

How to judge if heuristic is good or not?

Criteria for good heuristic functions

Admissibility - An admissible heuristic never overestimates the distance to the goal
Consistency - Consistent if, for each node n and its successor n’, cost function c, action a and goal state G, we have , similar as the triangle inequality in geometry
Roughly, we want the the heuristic to say

It is equal or more expensive to go from n to n’ than the goal directly when factoring in cost

A* Search

Best known form of best-first search

Avoid expanding expensive paths
Expand most promising first
Evaluation:
g(n) = cost so far to current node n
h(n) = heuristic estimate for cost to get to goal from node n
f(n) = estimated total cost through n to goal
Implementation: Frontier as priority queue by increasing f(n)

h(n) -> Heuristic could be straight line distance
g(n) -> Distance covered to get to node
f(n) -> A* estimation function

A* Seach is:

Complete IF consistent
Optimal IF consistent
Consistent -> Complete and Optimal (like BFS)

Minimax Algorithm

One tries to maximize score, the other tries to minimize

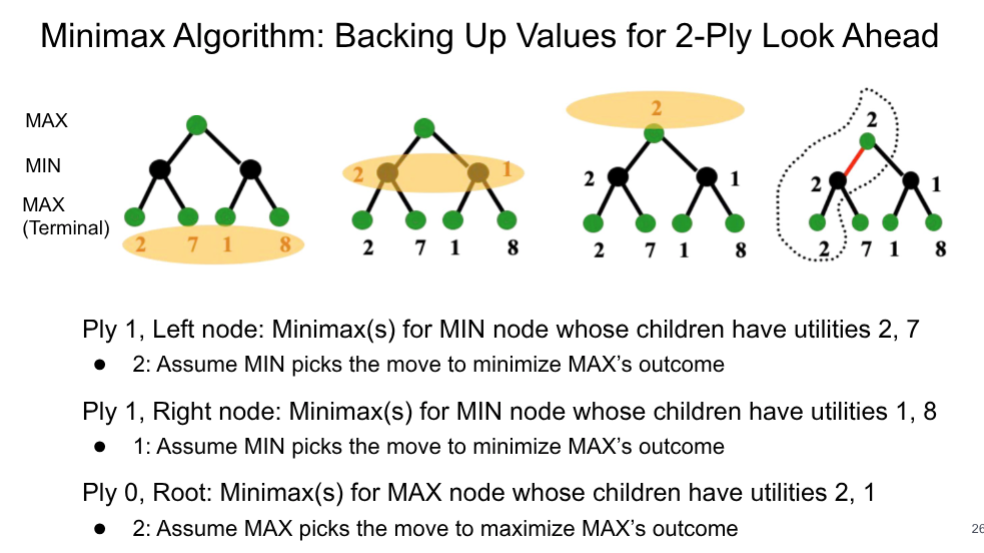
Not very efficient, need to expand a lot of leaf nodes

We introduce:

Alpha Beta Pruning

- Value of the best (highest-value) choice we have found so far at any choice point along the path for MAX
- Value of the best (lowest-value) choice we have found so far at any choice point along the path for MIN

In MAX node:

If current child value then its MIN ancestor above won’t consider this MAX node, so prune
Else update:
In MIN node:
If current child value then its MIN ancestor above won’t consider this MAX node, so prune
Else update:

Essentially:

In a MIN node: We know that a higher up MAX node won’t consider this MIN node if it has the option to choose a node of value that is less than the highest found so far.
In a MAX node: We know that a higher up MIN node won’t consider this MAX node if it has the option to choose a node that is greater than the smallest value found so far.

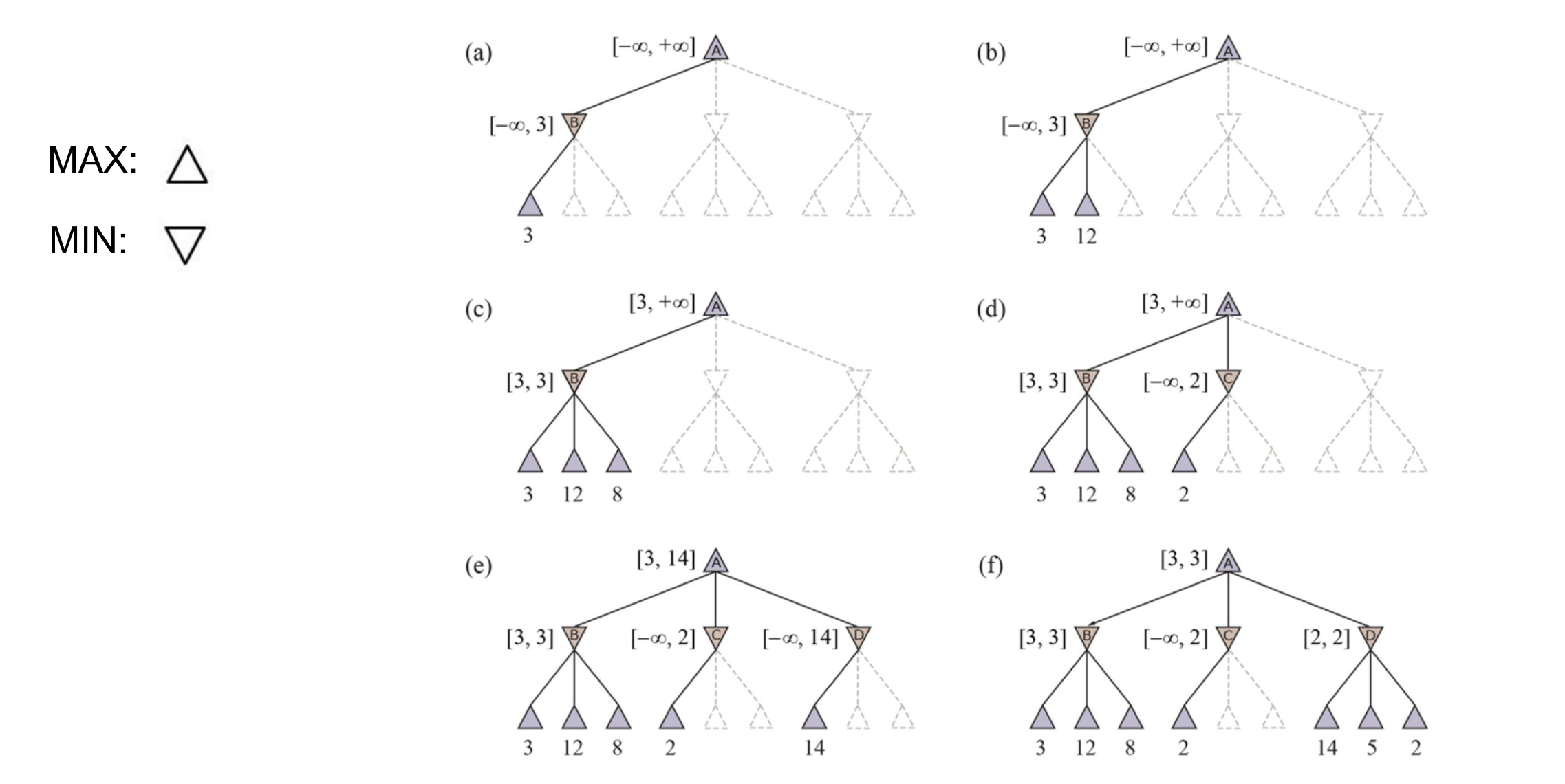
a) We explore our first leaf, and pass 3 as our smallest (best) value so far for our MIN node above, updating beta. ()
b - c) We continue exploring leaves, but find that there is not a value less than 3 so is not updated
c2) We update the alpha in the MAX node above, as the biggest (best) value it can choose so far is 3
d) We explore leaf nodes, and find 2 in the next MIN node. This means that no matter what, the value of this min node will be less than or equal to 2. Since we know this MIN node won’t be picked , we can skip the rest of the leaves entirely and move on. Algorithmically:

# from above
alpha = 3

# initializing
beta = float('inf')
for leaf in MIN node:
    val = leaf.val
    beta = min(beta, val)
    if beta <= alpha:
        break # we prune
return beta

e-f) We explore leaf nodes in the next MIN node, and find the smallest leaf to be 2. This will not be picked by the root MAX node, which will pick 3.

Four Steps of MCTS (Monte Carlo Tree Search)

Selection: Start from root R and select successive child nodes until a lead node L is reached
Expansion: Unless L ends the game (e.g. win/loss/draw) for either player, create on child node C
Simulation: Complete one random play-out from node C (also called play-out or roll-out). A play-out may be as simple as choosing uniform random moves until the game ends
Backpropagation: Use the result of the play-out to update information in the nodes on the path from C to R

Selection:

Select a node with the highest upper bound confidence bound of its utility
- - Exploitation term - average utility of n
- - It is high when this node has not tried much times, so it encourages exploration on this node
- is the total utility of all play-outs through node n
- is the number of play-outs through node n
- is the number of roll-outs at the parent node of n
- is a constant to balance the two terms

Core Idea of MCTS (from Wikipedia)

Find the most promising moves and expand the search tree.

Based on each selected path, play out the game to the very end by selecting moves at random.

The final game result of each playout is then used to weight the nodes in the game tree so that better nodes are more likely to be chosen in future playouts.

Hill Climbing

Blindly tries to maximize an evaluation function f(n), going up the function maximization hill one successor at a time

Given: current state , evaluation function , and a successor state , attempt to find a state that maximizes

If , move to
Else, halt at n
Chooses a random best successor if multiple
Terminates when a peak is reached

Has no look-ahead, and cannot backtrack

Simulated Annealing

Combine hill climbing with a random walk in a way that yields both efficiency and completeness

incorporate a random walk into hill climbing. Allow some ‘exploration’
- “Allows to pick an action that results in a worse state, but gradually diminishes this probability”
  Control parameter T, temperature
T controls probability of picking a worse successor
Start out high to promote escape from local maxima, then gradually decreases to zero

Beam Search

Hill climbing only keeps track of one best state
Beam search keeps track of k best states in memory

starts with k randomly selected initial states
Find successors of all k states
Take top k successors across all successors and put them in memory

Beam Search for Language Generation

Generate a sentence, and track the most promising completions over time

🧪 -> Refresh the Info

Did you generally find the overall content understandable or compelling or relevant or not, and why, or which aspects of the reading were most novel or challenging for you and which aspects were most familiar or straightforward?)

Did a specific aspect of the reading raise questions for you or relate to other ideas and findings you’ve encountered, or are there other related issues you wish had been covered?)

Vault

Explorer

ECS170-D9