ECS170-L27

📗 -> 06/02/25: ECS170-L27

---

Machine Learning Slides

🎤 Vocab

❗ Unit and Larger Context

Small summary

✒️ -> Scratch Notes

Underfitting vs Overffiting:

• Model not being complex enough to interpret data vs. overfitting and capturing as much of training data as possible while ignoring generalizability

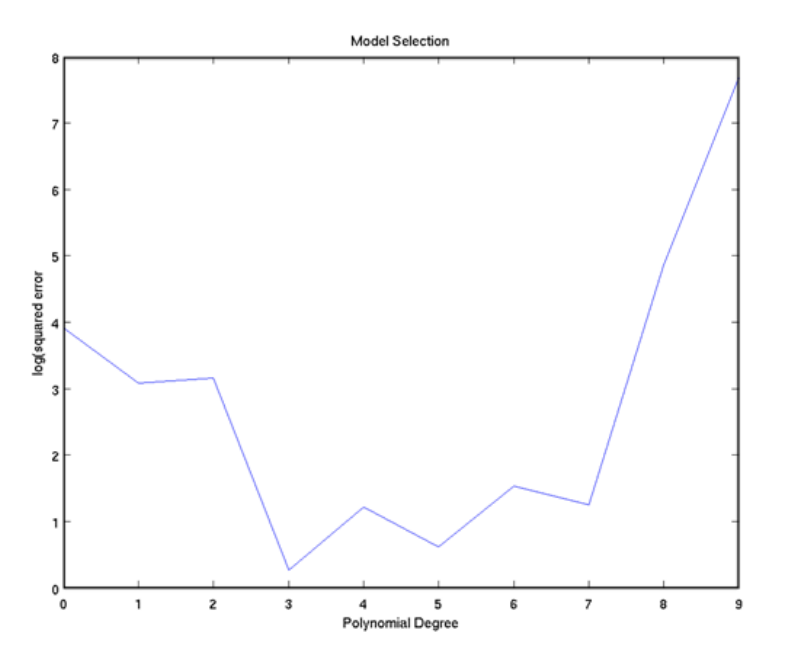
Polynomial Interpolation

Generate noisy training data from a simple function, then try to fit models of increasing complexity

• How does training error differ among models?
• Test error?
• Takeaways?
  Check how
• parameters magnitude motivates regularization
• Training size affects model
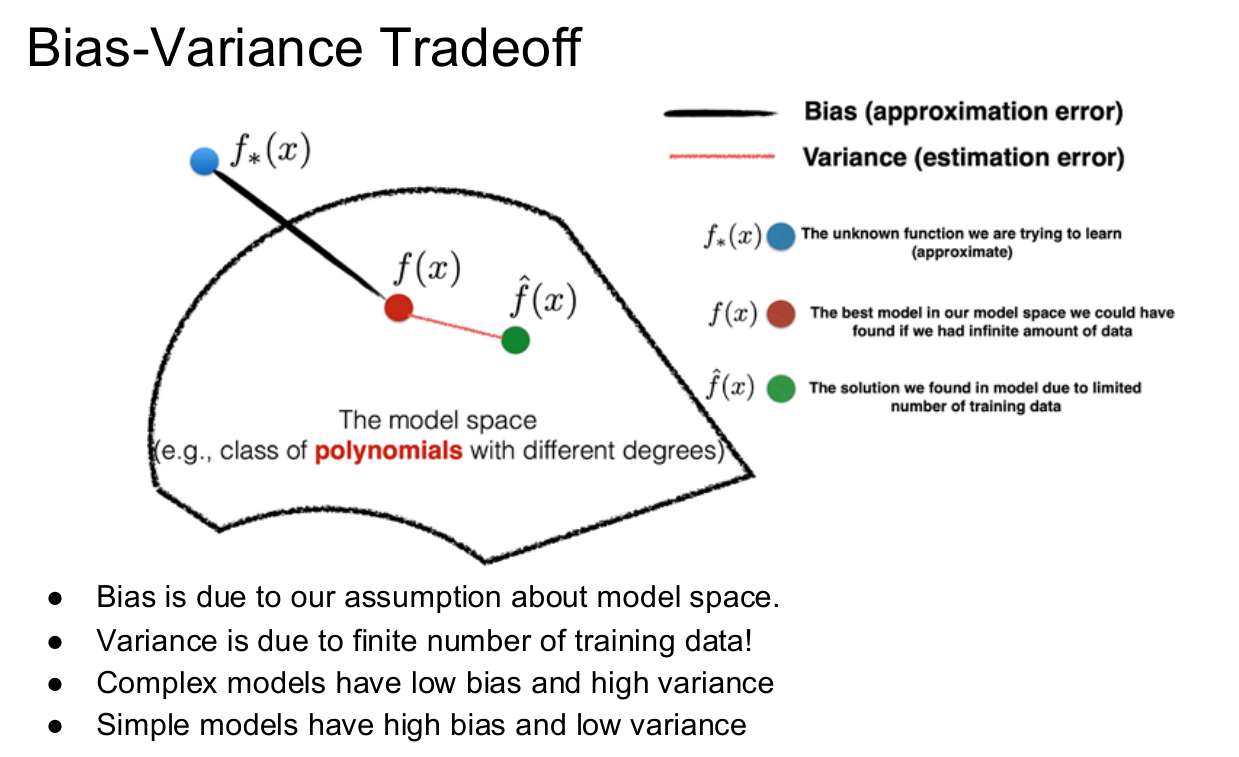
• Bias-variance (approximation-estimation) error decomposition

Toy data will be points sampled from a sine wave, plus an error term

Fitting Polynomials:

Fit polynomials of degree to the data
By increasing polynomial dimensions (p), the model becomes more complex (richer), and we will fit the weight terms

• 
  
  
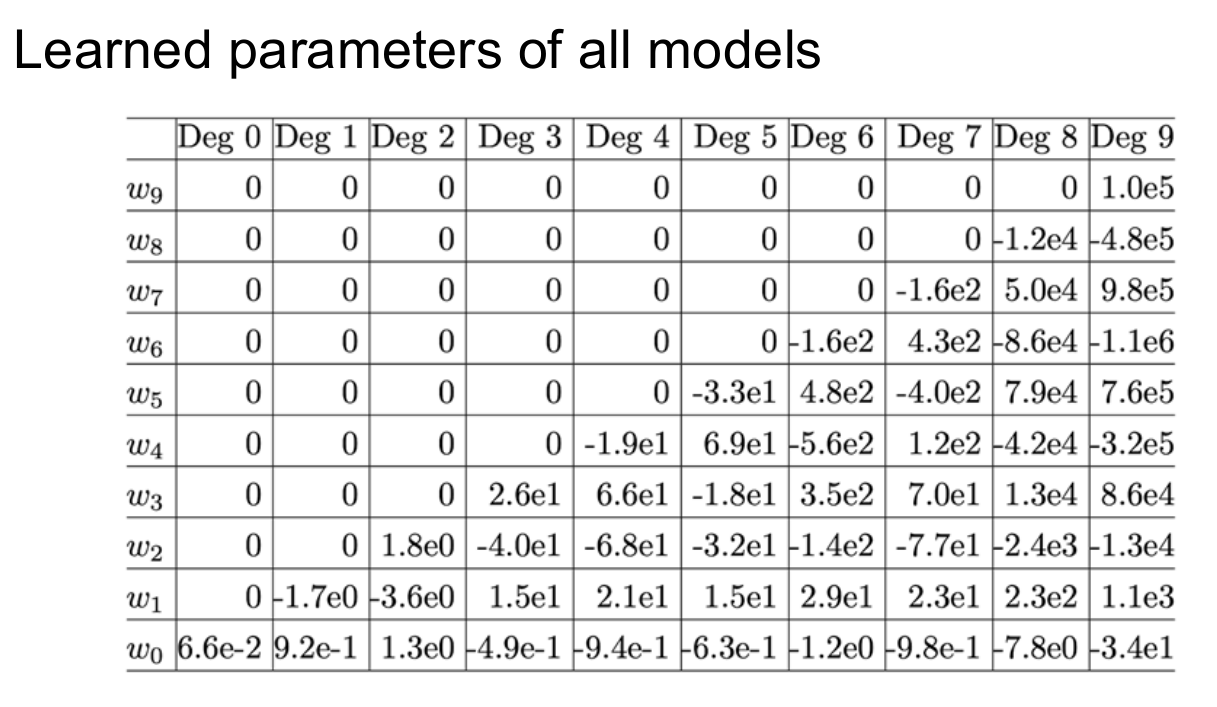
• Higher degree polynomial weights tend to be much larger than smaller degree polynomials

Analysis

Degree 9 fits all of the training points exactly. Zero training error.
Degree 0 polynomial does not do a good job of fitting data, essentially just the mean
Still, Degree 0 polynomial had lower generalization error than degree 9 polynomial

Degree 0 polynomials Degree 9 polynomials

• Degree 9 polynomials more complex, and more representation power

Why do we see this behavior?

• Bias - Roughly equal to expressive power: higher bias, lower expressive power
• Variance - Equal to how well parameters can be estimated: higher variance, higher expressive power
• Degree 9 polynomial fits all noisy training points exactly, trying to detect patterns in the noisy, and it overfits

Takeaways

1. Generally, can improve performance by restricting degree of freedom (such as number of parameters)
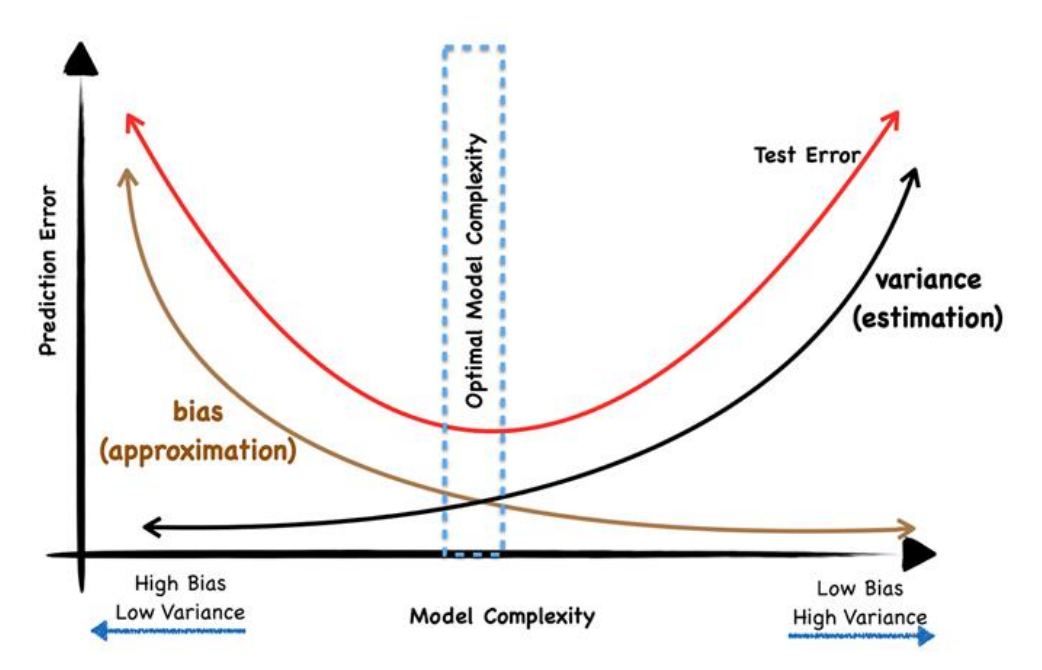
2. Generally, as number of parameters increases:
   • Model complexity increases
   • Bias decreases
   • Variance increases
3. Generalization error
   • Initially decreases: decrease in bias dominates increase in variance
   • Then increases again: decrease in bias becomes small while increase in variance becomes large

Next logical step: Increase training data

Data

With more data samples, the degree 9 polynomial becomes a pretty good estimator too!

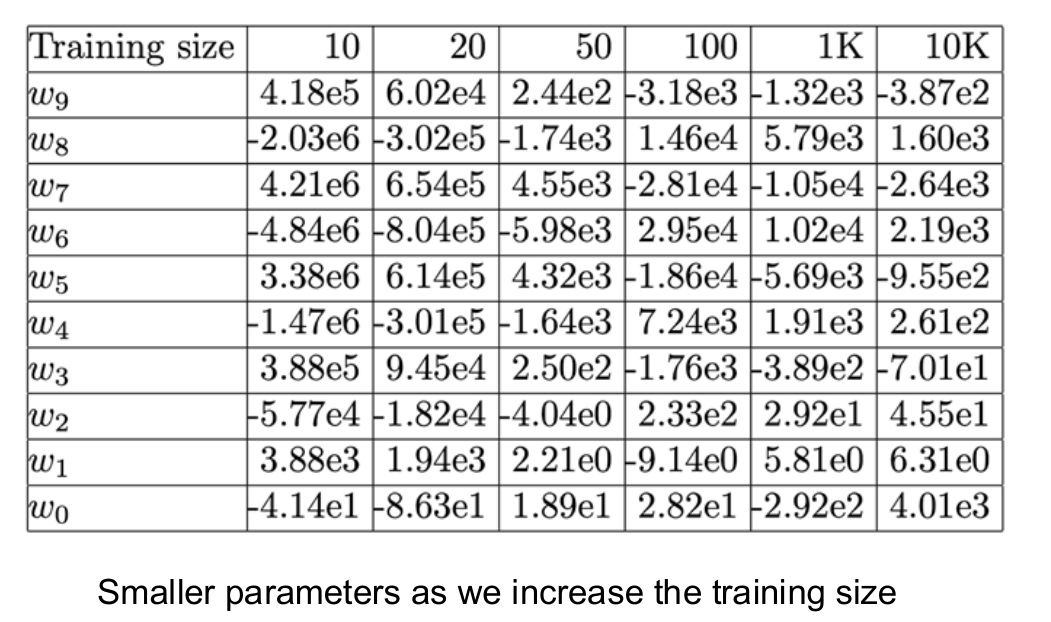
• Notice how the parameters get smaller
• Helpful because “if x changes slightly from a test case, it is likely that the y changes dramatically because of large x”. Remedy this tendency by having smaller weights, allows similar x-s to get similar estimations

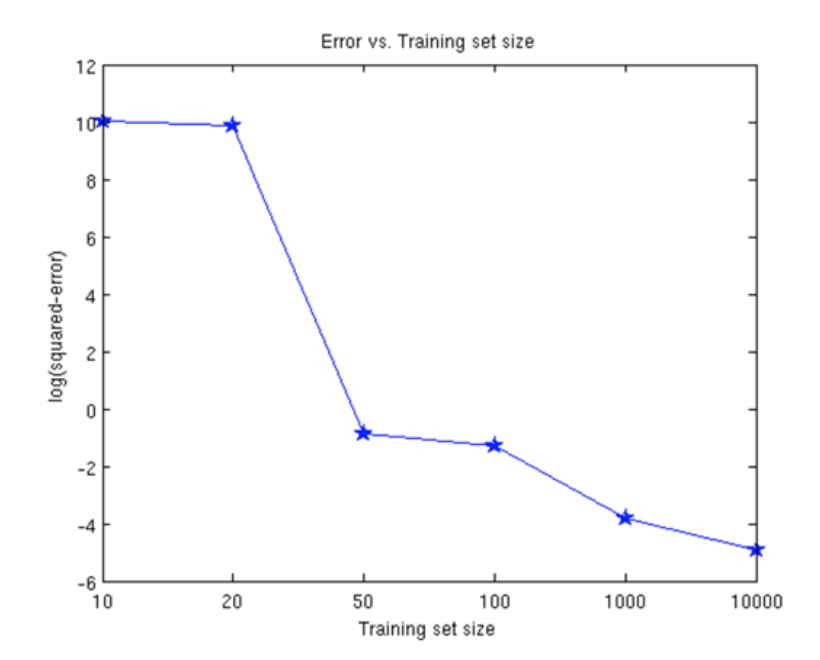
Error vs. Training Size

1. Generally, can improve performance by restricting degree of freedom (such as number of parameters)
2. Improve performance by getting more data:
   • Variance decreases
   • Bias unchanged, this is implicit to the model. Without changing model, this stays the same
   • Generalization error decreases
3. How else can we improve performance?
   • Restrict parameters
   • Add penalties for large parameters (we saw how they were prone to overfit)

Regularization

🧪 -> Refresh the Info

Did you generally find the overall content understandable or compelling or relevant or not, and why, or which aspects of the reading were most novel or challenging for you and which aspects were most familiar or straightforward?)

Did a specific aspect of the reading raise questions for you or relate to other ideas and findings you’ve encountered, or are there other related issues you wish had been covered?)

🔗 -> Links

Resources

• Put useful links here

Connections

• Link all related words