Q1
The model neurons we have looked at have a set of weights, w1 , … , wN , and a bias b. Given some inputs x1 , … , xN , they compute a total input z = w1 x1 + … + wN xN + b. They then pass this input through an activation function f to get the output.
We looked at two activation functions. The threshold activation allows neurons to be “off” (output of 0) or “on” (output of 1) but not to have different activity levels beyond that. Many biological neurons, however, communicate information based on how active they are. The ReLU activation function captures this by allowing the output of the neuron to take on a variety of values (any positive value). However, the output of a ReLU activation function has no limit (e.g., it can be 1, 000, 000) and biological neurons have a maximum firing rate.
(a) One way to model a maximum activity is by adding a maximum threshold to the neuron. For example, the activation function below has a maximum activity of 100.
Consider a neuron with two inputs, with weights w1 = 5 and w2 = 3 and bias b = −10 that uses this activation function. Find an input (i.e., values of x1 and x2 ) that gives an output of 0, an input that gives an output of 50, and an input that gives an output of 100.
(b) Plot the ReLU function and the function above on a graph, showing z on the x-axis and the output of the function on the y-axis.
a) Will be using coordinates to represent vectors of input activations:
Formula for z:
An activation that gives 0 is
An activation that gives 50 is
An activation that gives 100 is
b)
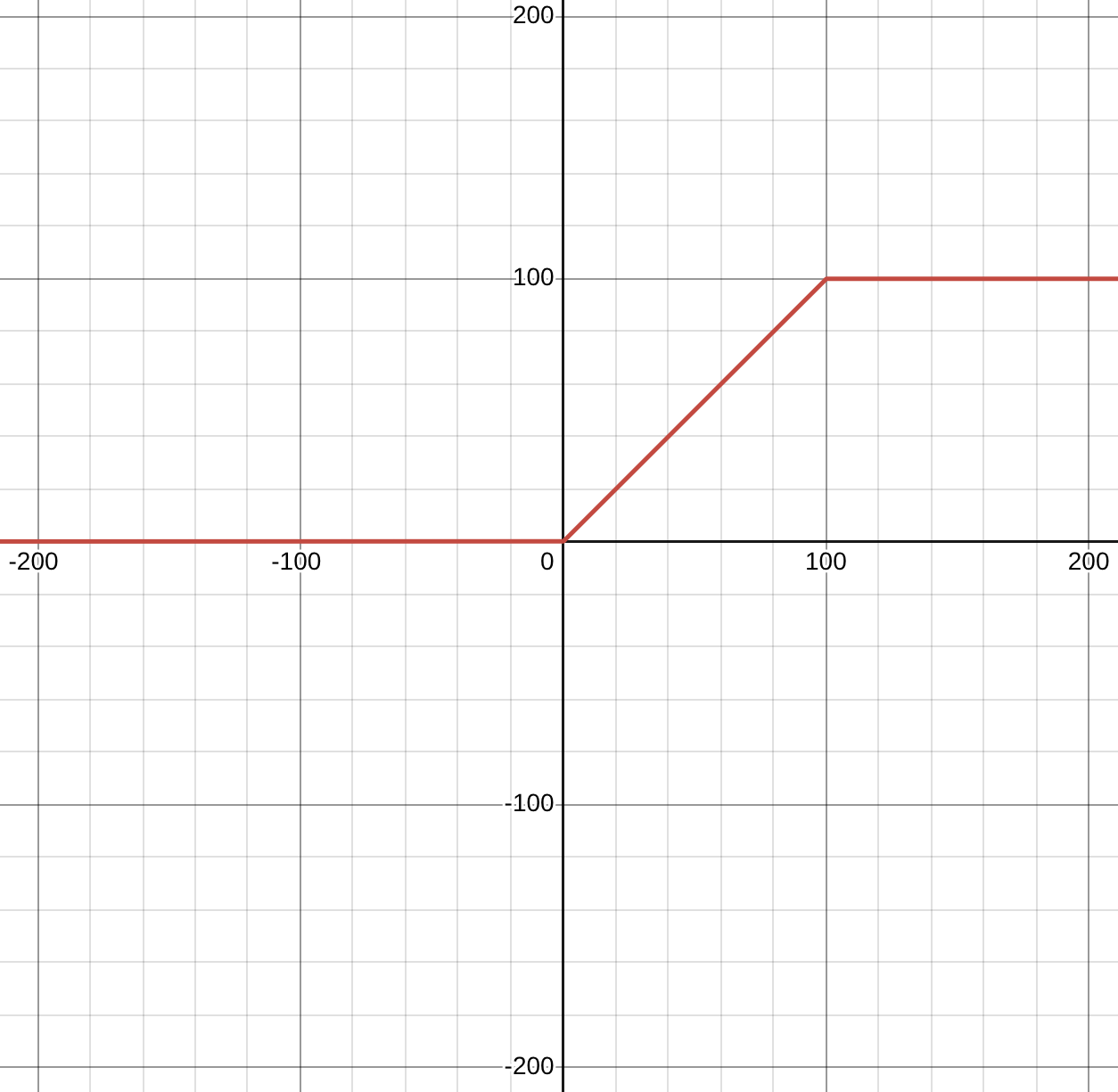
Plotted with function: min( max(0, x), 100)
Q2
The link for the single neuron models notebook is https://colab.research.google.com/drive/10voJh1kLvB-aW7IuY1qjltmcKIXXgIFa?usp=sharing (also found on Canvas).
(a) Spend some time running this notebook and reading through the code (no need to turn in anything for this part).
(b) At the end of the first section of the notebook it asks “Now consider a threshold neuron (perceptron) with both weights of 1 and a bias of -4. Can you figure out at which values of inputs (i.e., x1 and x2 ) the neuron switches from being off (i.e., output 0) to being on (i.e., output 1)? Do you see any pattern?”
Using the notebook, find some values of input for which the perceptron is right on the threshold between an output of 0 and an output of 1. Find a pattern in these values and use this pattern to explain why the boundary between the output of 0 and the output of 1 is a line.
b)
It switches to on when the following equation is true:
- Examples of satisfying inputs to activate neuron:
The threshold of the perceptron’s output is defined by the line:
- Inputs where the above is satisfied lie exactly on the decision boundary.
This is the case because a perceptron is a linear classifier, arriving at its classification by by scaling inputs linearly and combining them, along with a bias. Due to not introducing any nonlinearity, the perceptron can only create a linear classification of the input data.
Q3
Here is a link to a notebook that implements a simple perceptron (but no learning) https:// colab.research.google.com/drive/1TD7gXBZExwSOW-G29p9HiYCY4-zhHBSE?usp=sharing (also found on Canvas).
(a) Spend some time running this notebook and reading through the code (no need to turn in anything for this part).
(b) At the end, the notebook gives you some data and ask you to find a perceptron that is able to correctly classify all the data points. What weights and bias do you find? Draw a picture of the regions which it classifies as 0 and which it classifies as 1 (you can copy this from the graph in the notebook once you’ve found it). Note that for this problem you are finding the weights by trial and error rather than using the perceptron learning rule.
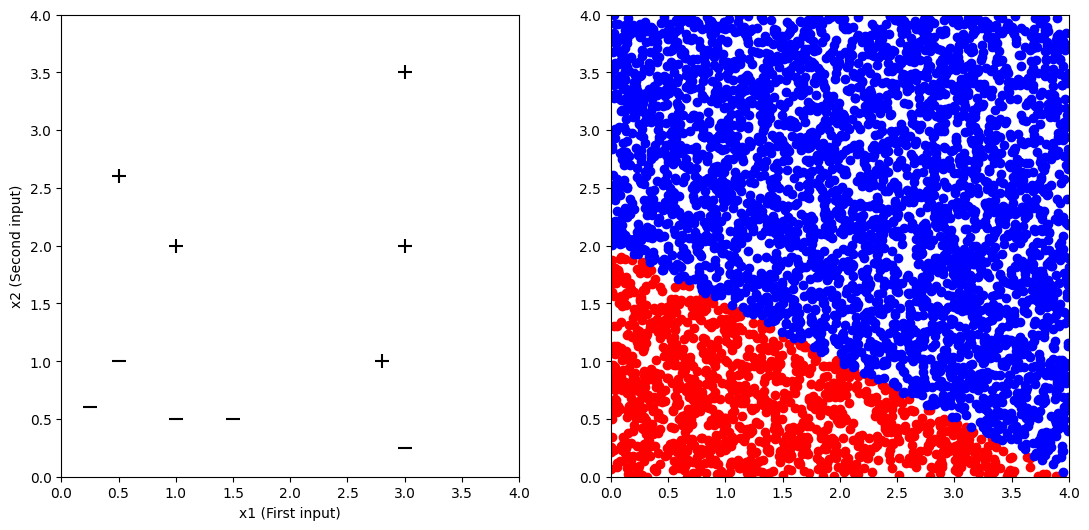
Perceptron formula used: perceptron(x1, x2, 1, 2, -4)
No mistakes made on the input data:
x1 x2 correct output perceptron output
0.25 0.6 0 0
0.5 1.0 0 0
1.0 2.0 1 1
1.0 0.5 0 0
3.0 2.0 1 1
3.0 3.5 1 1
1.5 0.5 0 0
3.0 0.25 0 0
2.8 1.0 1 1
0.5 2.6 1 1
Number of mistakes 0
Q4
The perceptron learning rule we’ve seen so far updates weights as
w(t + 1) = w(t) + e(t)x(t),
where w(t) is the weight at time t, x(t) is the input at time t, and e(t) is the error at time t (we’re ignoring biases for simplicity). Typically, however, one adds a parameter to control the size of the changes to connection weights and biases. Thus a more typical learning rule (again ignoring biases) would look like
w(t + 1) = w(t) + αe(t)x(t),
Here the parameter α is called the learning rate.
(a) When might you want a small vs. large learning rate? What are the advantages and disadvantages of each?
(b) The learning rate can be kept fixed over time, but often in practice one starts with a large learning rate and then makes it smaller over the course of learning. Why might one do this? Can you think of any parallels to this strategy in biology or cognition?
a)
The learning rate scales the magnitude of the updates made by the perceptron. A large learning rate means that the perceptron can make large updates on each error it makes (analogous to being highly adaptable). A small learning rate means that the perceptron only makes small updates on each error (analogous to sticking to the same strategy).
Each has its advantages:
- A large learning rate helping a perceptron quickly move away from bad weights. However, it makes the weights a perceptron arrives it fragile, and can make the perceptron abandon working strategies. Additionally, it can make updates ‘overcompensate’ and might not arrive at a good compromise between weights.
- A small learning rate helps a perceptron make strong updates at each iteration, with high security it won’t overshoot a working solution. Additionally, it is not as prone to abandoning working strategies, with small updates being less likely to lead to a disastrous update. However, it has the disadvantage of being extremely slow to train, requiring many iterations to make the same update as a large learning rate.
b)
It can be advantageous to have a high initial learning rate to move towards a good starting place for the network (moving into a sensical starting position) before decreasing the learning rate to finetune it from there. This is analogous to using the knobs to tune a violin, before switching to the fine-tuners when you’re almost fully tuned.
In cognition, this could be advantageous to have a high learning rate as a kid to absorb as much information as possible, before decreasing it in adulthood so that information can be preserved and finetuned from there.
Q5
The diagram below shows a small network of 3 perceptrons, labeled 1, 2 and 3. All three use the threshold activation function, so their outputs are either 0 or 1. The network receives two inputs, x1 and x2 . Perceptron 1 receives the two inputs with weights w1 and w2 and has bias b1 . Perceptron 2 receives the same two inputs but with weights w3 and w4 and has bias b2 . Perceptron 3 receives the outputs of perceptron 1 and 2, with weights w5 and w6 and it has bias b3 . The output of perceptron 3 is y (which is the output of the network).
Let w1 = 2, w2 = −3 and b1 = −1; w3 = −2, w4 = 1 and b2 = 2; w5 = 2, w6 = 3 and b3 = −2. If the inputs to the network are x1 = 1 and x2 = 2 what are the outputs of perceptron 1 and 2? What is the total input (z) to perceptron 3? What is the output of the network as a whole?
Formula for inputs:
Working through the calculations:
Resulting values:
- Perceptron 1: z=-5, and produces an output of 0
- Perceptron 2: z=2, and produces an output of 1
- Perceptron 3: z=2, and produces an output of 1
Q6
A classic simple problem that a perceptron cannot solve completely is called the XOR problem. In this problem there are 4 data points. Each data point consists of two inputs and a label. For an example of this problem, consider the points (0, 0) with label 1, (0, 1) with label 0, (1, 0) with label 0, and (1, 1) with label 1.
(a) Plot these 4 points showing the value of the first input along the x-axis and the second along the y-axis. Mark points that get a label of 0 with a minus sign and those that get a label of 1 with a plus sign (similar to the lecture). What is the best line you can draw separating the − points and the + points? Explain why a single perceptron cannot solve this task.
(b) Now imagine trying to solve this problem with the 3 perceptron network shown in Problem 5, meaning that the output of perceptron 3 should give you the correct label for each pair of inputs. Can you find weights and biases for the three perceptrons that solve this problem?
a)
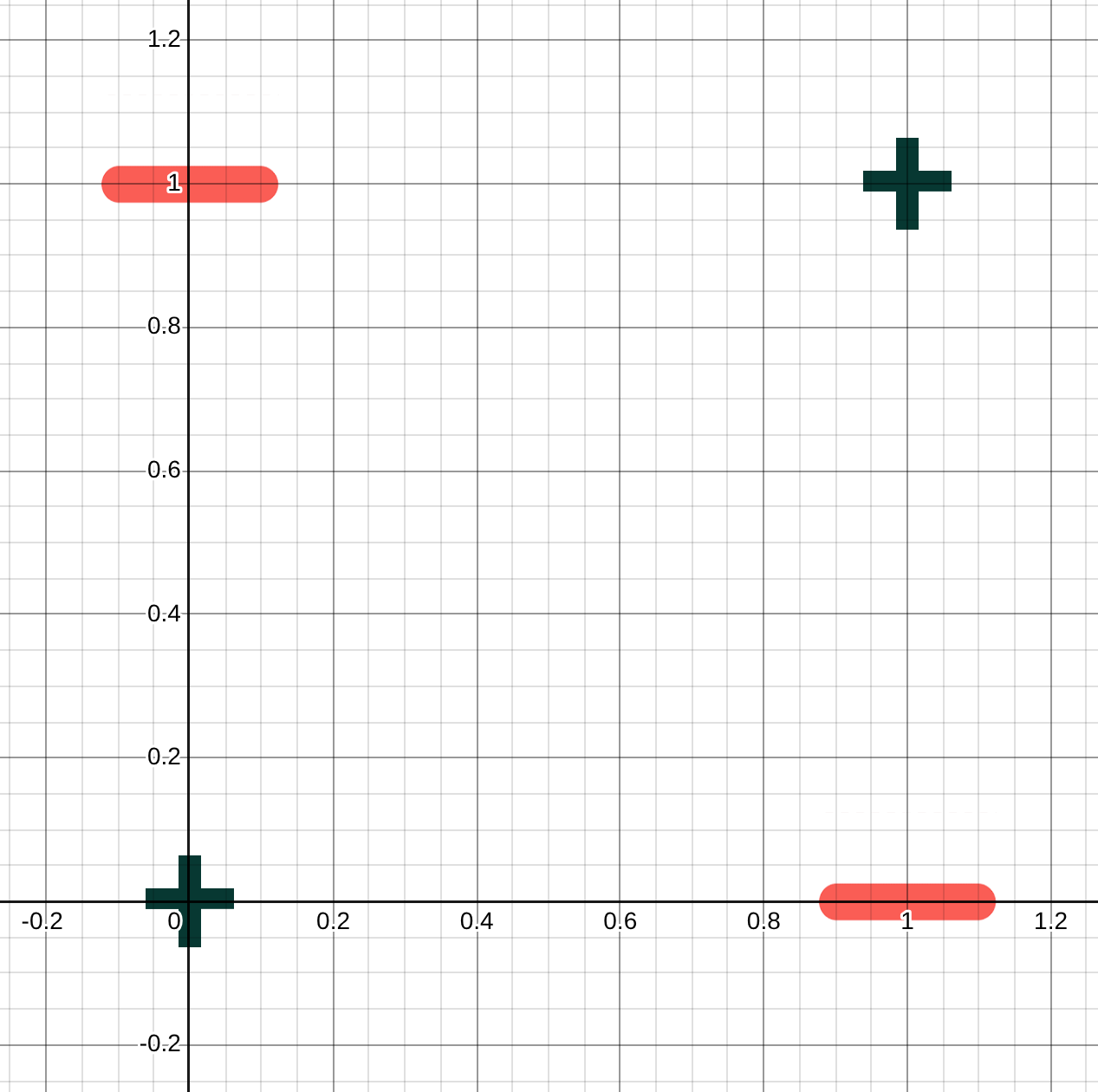
The best line you could draw to separate them would only get three of the four points correct, there is no line that could get them all correct. A perceptron is a linear classifier, and the points are not linearly separable (divisible with a line).
Example of best line:
Classifications:
| Point | Actual | Correct | Correct |
|---|---|---|---|
| (0,0) | 1 | 0 | ❌ |
| (1,0) | 0 | 0 | ✅ |
| (0,1) | 0 | 0 | ✅ |
| (1,1) | 1 | 1 | ✅ |
b)
This solution is essentially an AND of a OR perceptron and a NOR percetron (
Using the threshold activation function:
| z1 | f(z1) | z2 | f(z2) | z3 | f(z3) | Label | |
|---|---|---|---|---|---|---|---|
| (0,0) | 0 | 0 | 0.5 | 1 | 0.5 | 1 | 1 |
| (1,0) | 1 | 1 | -0.5 | 0 | -0.5 | 0 | 0 |
| (0,1) | 1 | 1 | -0.5 | 0 | -0.5 | 0 | 0 |
| (1,1) | 2 | 1 | -1.5 | 0 | -1.5 | 1 | 1 |
Q7
The link to the ReLU notebook from the Week 3 coding/discussion section is here: https:// colab.research.google.com/drive/1vWh8lQf0ajFlYANrUT_PdLI7Qw2CweOs?usp=sharing (also found on Canvas). It asked your group to put together a function for a rectified linear neuron. It then asked you to set up a neuron that took two inputs and returned their average.
(a) Copy over or write out the code for your relu neuron function.
(b) What weights and bias did you find for a neuron that took two inputs and returned their average?
a)
Code for a relu neuron:
def relu_neuron(x1, x2, w1, w2, b):
z = w1*x1 + w2*x2 + b # Calculating activation
f_of_z = max(0, z) # ReLU
return(f_of_z)
b)
Code for an averaging neuron, assuming no negative inputs as instructed.
w1 = 0.5
w2 = 0.5
b = 0
relu_neuron(x1, x2, w1, w2, b)
Q8
To help you start to think of ideas for a final project, list one topic in neural networks or machine learning you are curious about (either something we have discussed in class or not) and two questions about this topic you have.
Im curious about explainable AI (XAI), and about what the bleeding edge of XAI looks like. Im familiar with some of the basic techniques in XAI look like (dimensionality reduction, maximum activations for specific neurons in visual nets) but am otherwise unaware of what modern XAI looks like.
Specifically, I’m curious about:
- If XAI has utility in the modern tech landscape
- What approaches towards XAI have been explored and what do current models look like?