ECS124-Final-Prep

Review Seshes

wed 3/12 - Link

Content Review:

• Suffix Trees
• Optimality Recurrence
• BLAST Hash Tables
• Additive Matrix
• UPGMA

thursday 3/13 - Link

Content Review:

• MT 2
  • 5b part 3
  • part 2d
• Writing pseudo code?
• Light perl scripting?

friday 3/14 - Link

saturday 3/15 - Link

ECS124-Final-Prep 2025-03-17 16.03.31.excalidraw

Content

Labs:

1. 1
2. 2
3. 3
4. 4

Midterm 1

Sequence alignment

• Global / Local / Semi-global
  • Global: Needleman–Wunsch algorithm
  • Local: Smith-Waterman
  • Sem
  • Biological uses for each one
• Longest common substring and subsequence
  • How do LCS and global alignment relate?
    Blast
    Recurrence relations
    Runtime analysis (Big-O)
    Writing code - Perl and Python
• Working with files, opening/writing/reading
• Regex, matching and replacing

Midterm 2

Clustering and Trees
Bayes Method
K-means
De Bruin Graph

• Genome assembly?
  Suffix Trees
• Common sequences between paths

Post Midterm 2

Hierarchical Clustering

• UPGMA
• Nearest neighbor
• General probability of a path and model combo.
• Viterbi algo

Ultrametric Tree

• A tree where all leaves are equidistant from the root

• In an ultrametric tree, the two longest distances among any three points must be identical.

• • There is no unique maximum, it will repeat

• Matrix M is only ultrametric if the maximum value in any 3 rows is not unique
  UPGMA - Unweighted Pair Group Method with Arithmetic Mean

• Go through a matrix combining rows/columns as you combine nodes (species/taxa)

• Combines the ‘closest’ neighbors iteratively

  • A and B make node AB combined

• With an ultrametric matrix, it will create a tree that is ultrametric and additive

• Additive trees

  • Use the four point test to test for additivity
    

    Transclude of ECS124-L14-2025-03-04-18.33.05.excalidraw

    
    
  • However, can be difficult, because for a matrix with 5 points, you need to test 5 groupings (5 choose 4 = 5)

• Jukes Cantor

Nearest Neighbor?
Neighbor Joining

Hidden Markov Models
Viterbi

• The viterbi algorithm is a Dynamic Programming algorithm that uses a hidden markov model and its transitions to find the most likely path to have produced emissions. It iteratively goes through the most likely thing to have emitted a character at every stage, and finds probability for both models
  
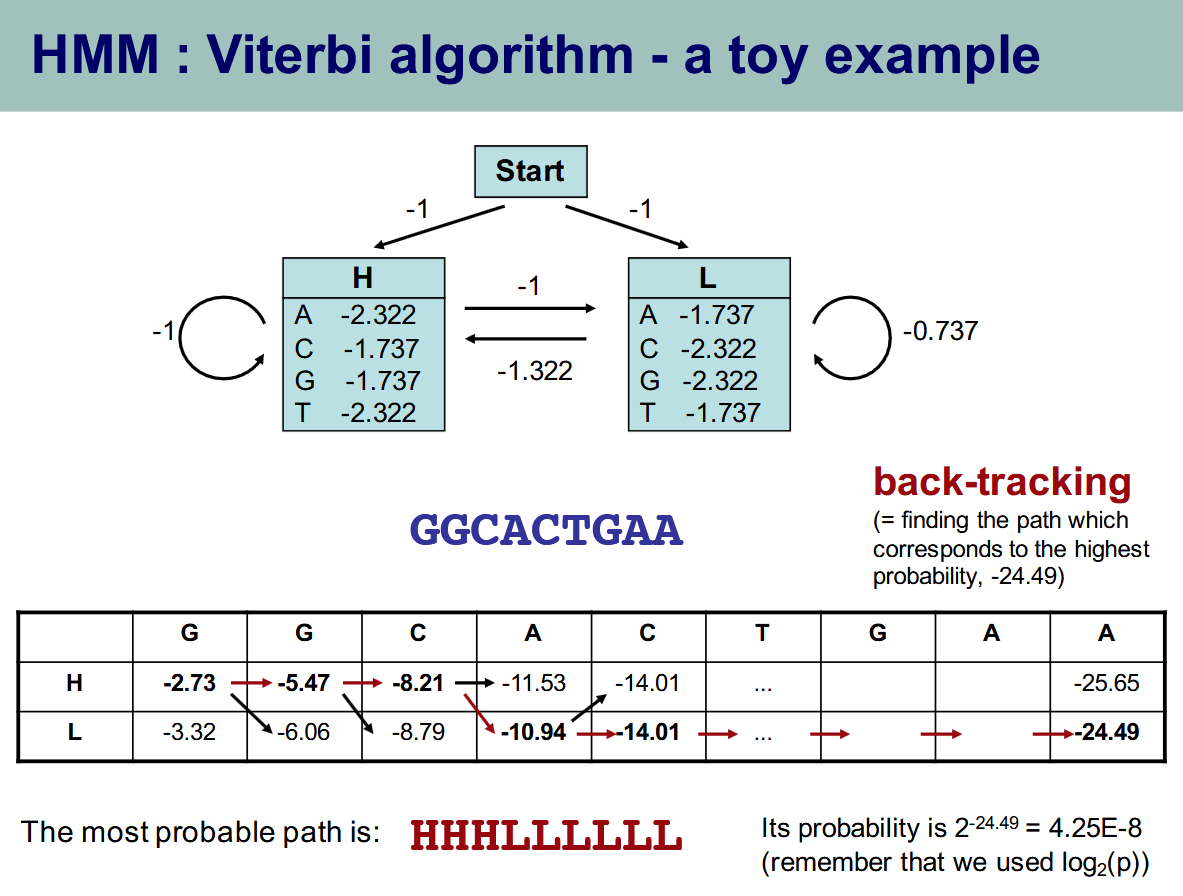
• Uses the max probability of arriving to a state, factoring in the immediately preceding state. Linear time, DP, very cool!

	A	B	C	D
A		8	5	4
B			7	3
C				2
D
Nearest joining:

r(i) = d(A,C) + d(B,C) + d(C,C) + d(D,C)

• 6+7+0+2 = 15 / 2 = 7.5
  r(j) = d(A,D) + d(B,D) + d(C,D) + d(D,D)
• 4+3+2 + 0 = 9 / 2 = 4.5
  D(C,D) = 2 - 7.5 - 4.5 = -10

UPGMA

	A	B	C	D
A	0	2	4	6
B		0	4	6
C			0	6
D				0

Heigh of AB is the average of their cluster distance

dist(AB,C) = ( D(A,C) + D(B,C) ) / 2 = 4
dist(AB,D) = ( D(A,D) + D(B,D) ) / 2 = 6

	AB	C	D
AB	1	4	6
C		0	6
D			0
D(ABC, D) = ( D(AB, D) + D(C, D) ) / 2 = 6

• Distance between old node (AB) and new node (C) to D

	ABC	D
ABC	2	6
D		0

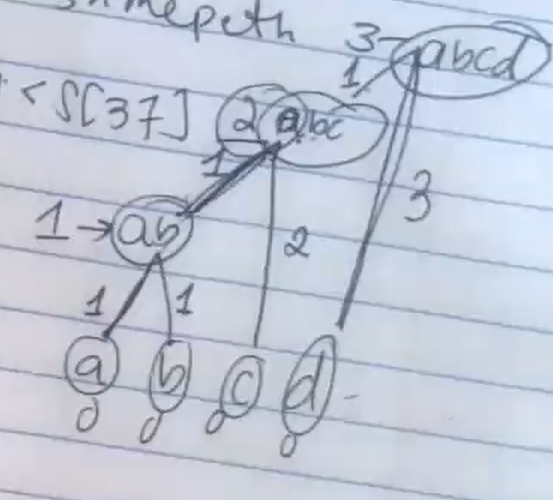
• Makes this tree at the end.
• Final height is 3