Dataview

LIST
FROM #Collection
WHERE file.name = this.Entry-For

White-Box Transformers via Sparse Rate Reduction

🎤 Vocab

❗ Information

Title:

White-Box Transformers via Sparse Rate Reduction

Abstract:

In this talk, we contend that a natural objective of representation learning is to compress and transform the distribution of the data, say sets of tokens, towards a low-dimensional Gaussian mixture supported on incoherent subspaces. The goodness of such a representation can be evaluated by a principled measure, called sparse rate reduction, that simultaneously maximizes the intrinsic information gain and extrinsic sparsity of the learned representation. From this perspective, popular deep network architectures, including transformers, can be viewed as realizing iterative schemes to optimize this measure. Particularly, we derive a transformer block from alternating optimization on parts of this objective: the multi-head self-attention operator compresses the representation by implementing an approximate gradient descent step on the coding rate of the features, and the subsequent multi-layer perceptron sparsifies the features. This leads to a family of white-box transformer-like deep network architectures, which we call CRATE, which are mathematically fully interpretable. Experiments show that these networks, despite their simplicity, indeed learn to compress and sparsify representations of large-scale real-world image and text datasets, and achieve performance close to highly engineered transformer-based models, including ViT and GPT2.

Bio:

Sam Buchanan is a Research Assistant Professor at the Toyota Technological Institute at Chicago (TTIC). He obtained his Ph.D. in Electrical Engineering from Columbia University in 2022. His research develops the mathematical foundations of representation learning for high-dimensional data, and applies these principles to design scalable, transparent, and efficient deep architectures for problems in machine learning and computer vision. He received the 2017 NDSEG Fellowship, and the 2022 Eli Jury Award from Columbia University.

✒️ -> Scratch Notes

White-Box Transformers via Sparse Rate Reduction

Part One: Theoretical Principles for Learning Representations

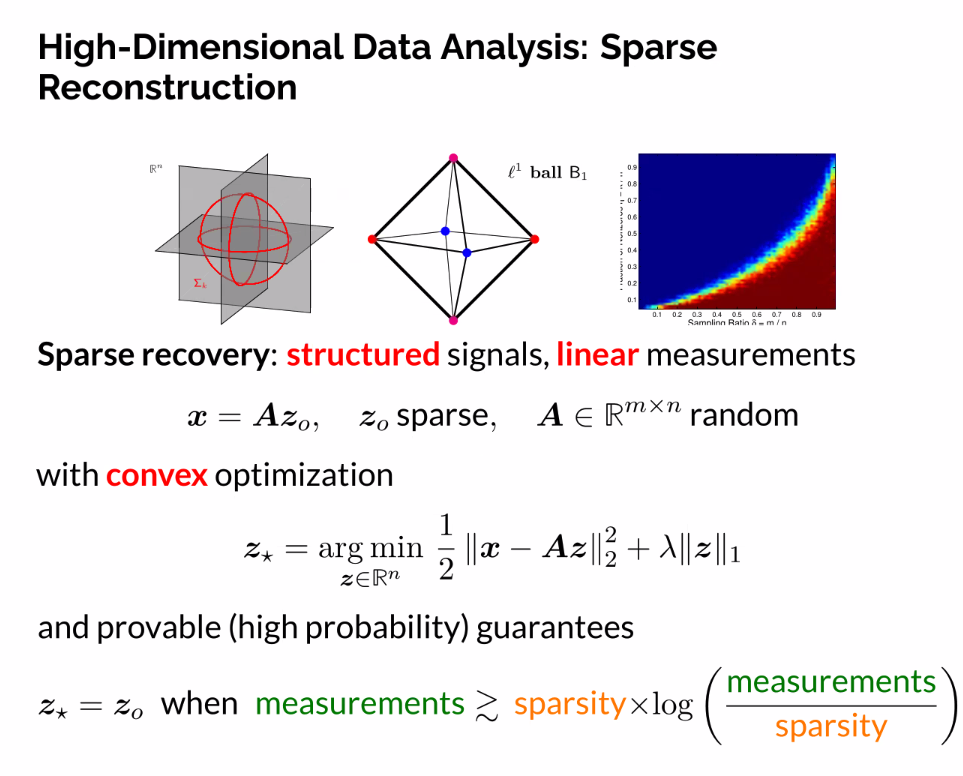
High dimensional representations with low dimensional encoding
LASSO
- Trade off ‘fiel’ representation to get a sparse representation
- Before DL this representation was SOTA

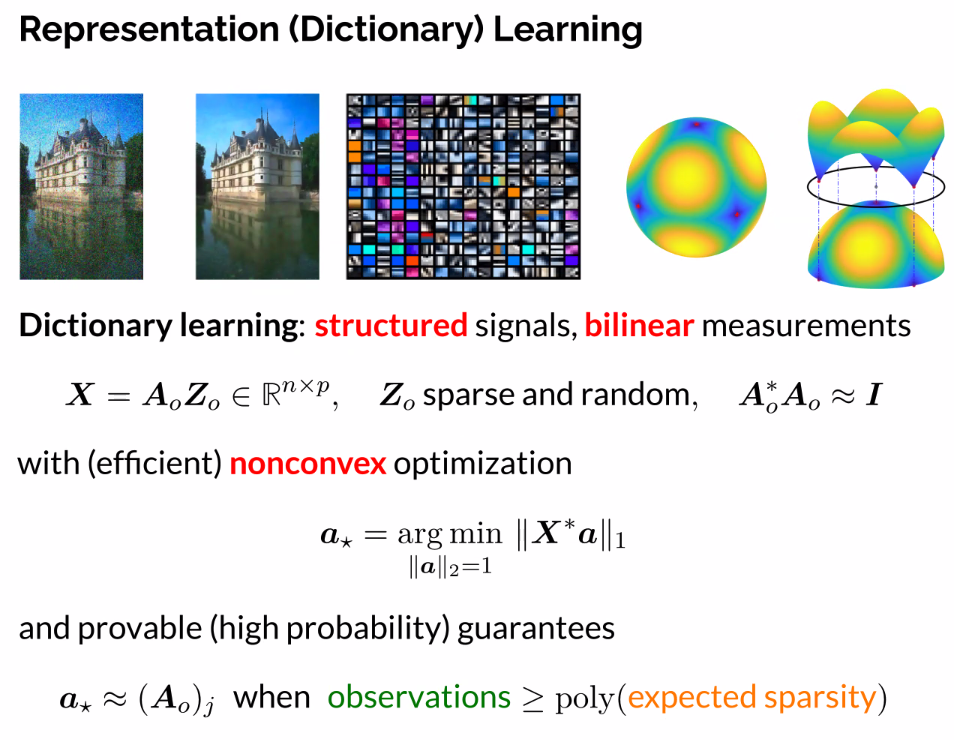
Now, modern deep representation learning:

Perceiving the physical world -> nonlinear signals
- Real world requirement of dealing/working
Nonlinearity demands deeper representations

Transformers: A universal Backbone

Helping in:

NLP
- BERT, GPT
Vision
Robots

Pitfalls of Black-box models

Transfomers are emperically-designed (or black-box models)
Q1: “How to understand such ‘emergent’ phenomena?”

Learning emerges in training, why? Black box stops us from knowing

Q2: How to mitigate such risks and ensure safety?

If we don’t know what internal computations are, we might get undesirable (even unsafe) outputs
Understanding internals is a must

Representations: What and how to learn?

Identify low-dimensional structures in sensed data of the world and transform to a compact and structured representation

The pursuit of low dimensional structures, using them for down stream tasks

Outline:

Analytical Models
General Distributions
- Denoising-Diffusion
- Compression and Information Gain
Network Architectures via Unrolling
- Create objective functions of representation, and optimize them
- Gradient descent on an objective function of representation
- Resemble layers of a Deep NN?

A low dimensional subspace:

What is a linear structure?

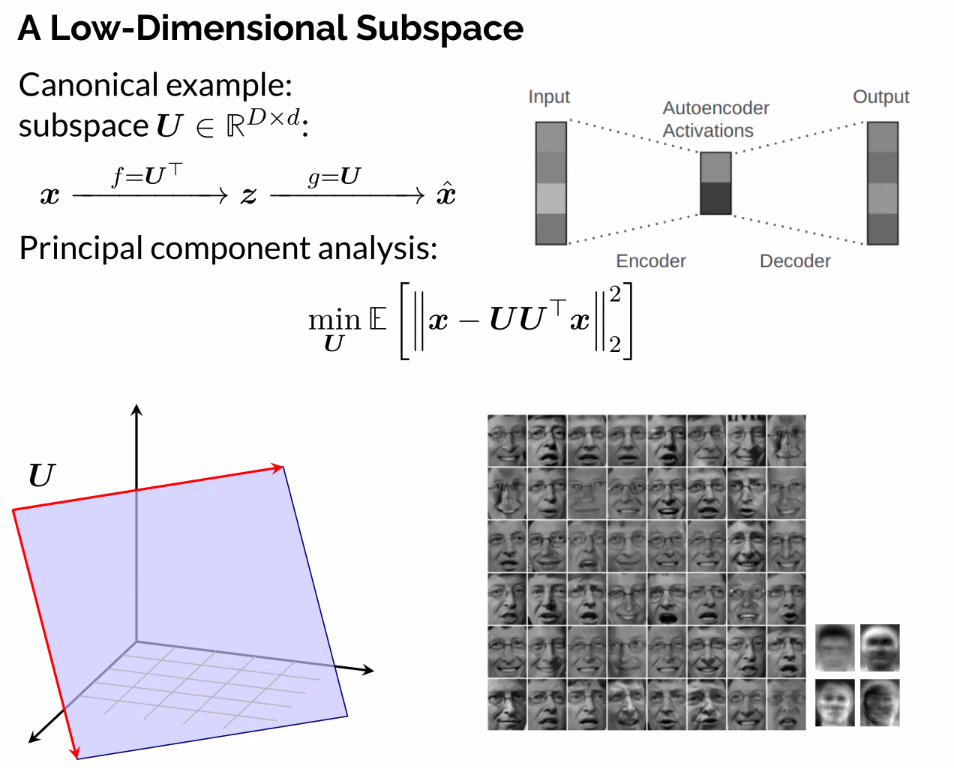
X: Columns of data matrix
Learn the subspace that the data lies on by solving the optimization problem
Linear structure of the data, and once learned, go from encoding to decoding
- Encoder is a projection
- Deco
All the primitavies of a more general learning scheme

Sparsity and Sparse Coding

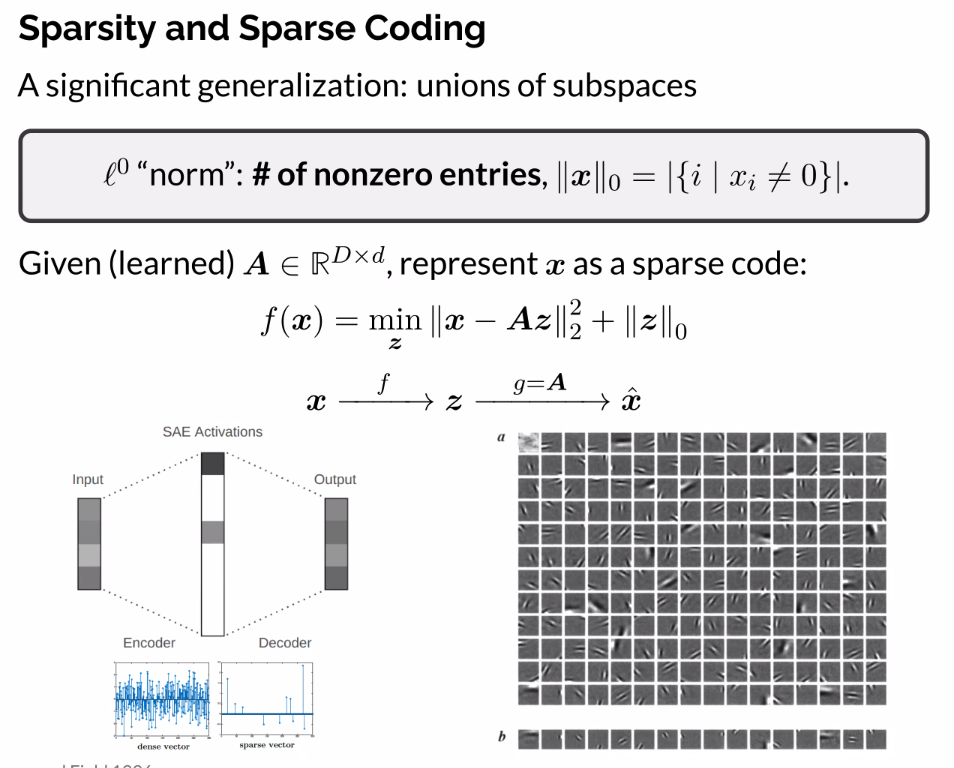
Encoder solving sparse coding problem
If we know apriory x, we can just solve

The way to solve:

How to learn: Optimization for low-dim structures

One step beyond gradient descent:
Sparse coding with (proximal) gradient descent

Given current code , gradient descent to better fit x
Without moving too much, sparsify the updated code
Then where

From analytical models to transfomers: Compression

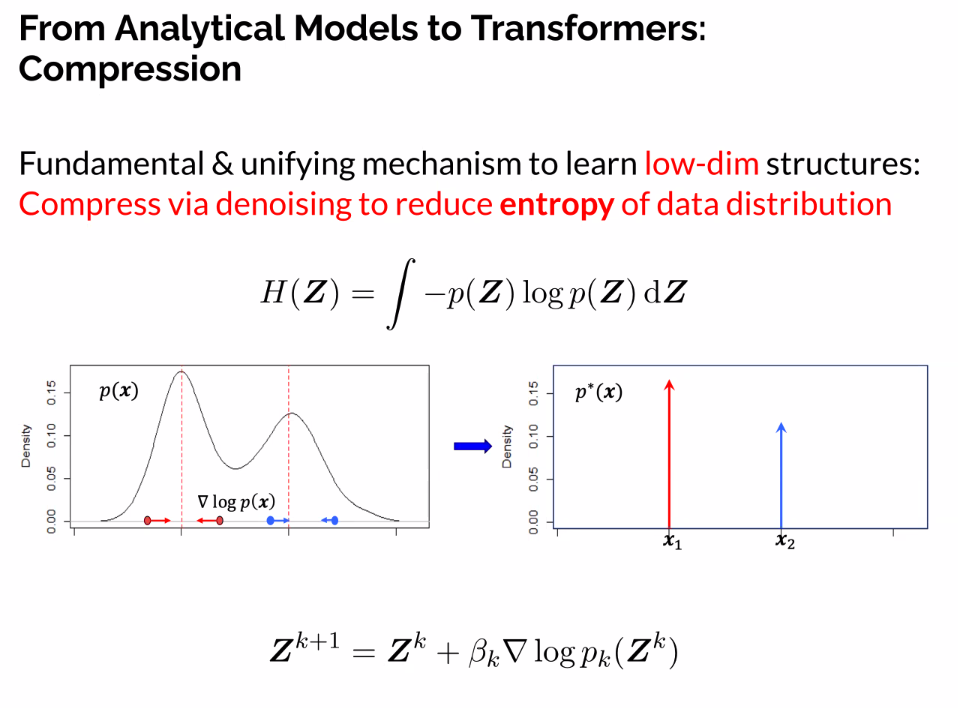
Intuitively: Try to reduce the entropy of the data
- Low entropy correlates lower dimensional representation of the data

Fundamental Primitive: Diffusion and Denoising

Piecewise linear?
Independent noising observation
Pass a noisy representation through a mapping, and seek to reduce the noise
Median Mean Squared Error (MMSE) Denoising problem
Tweedie: Closed form for a MMSE denoiser
- Not on slide, but should be expectation
- Simple to write, but complex in form
- Takes noisy input z, perturbs it in a score function
  - Need to do learning to recover score function
- Weighted by all the possible places the data ‘could’ have come from?

Denoising Against Low-Dimensional Structures

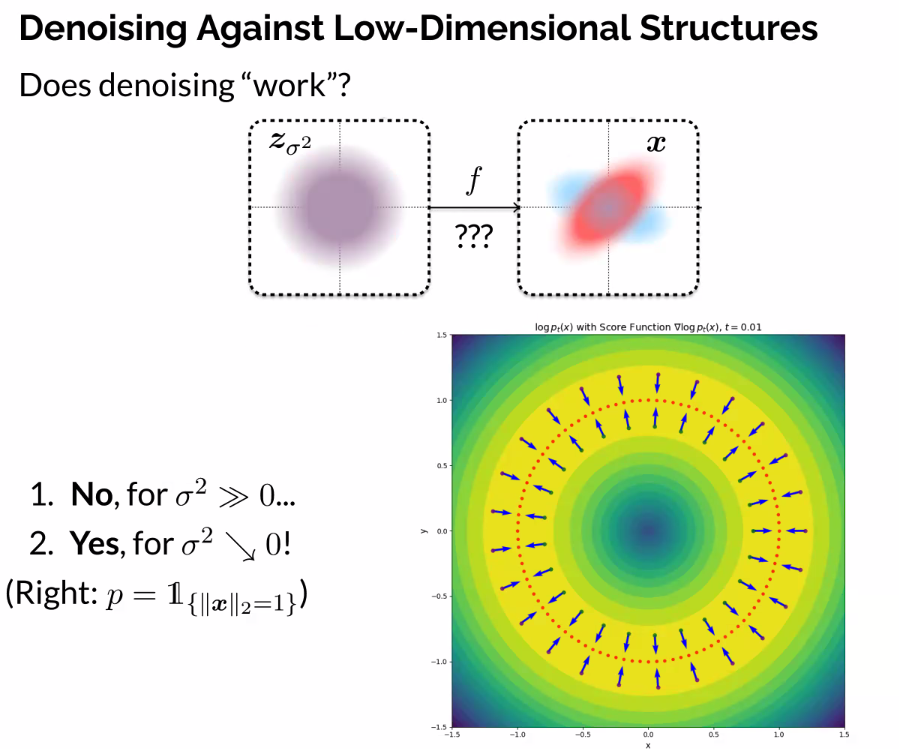
Intuitively, too much noise destroys distribution
If you add an imperceptible amount of noise, you can remove it
Think of a data distribution on a circle, then add a small amount of noise.
- The blue arrows are the score function (gradient log p), and pointing us towards the score of the data
- Point back towards underlying data manifold, will recover signal
- However, add too much we can’t tell which side of the circle we came from.
A toy example to build intuition
“Critical radius”

The entropy increases as we add noise
Removing noise, actually decreases entropy
- In a perfect sense, doing an ideal denoising function

Key to a number of things
Take derivative of entropy
REplace derivate of time with space derivate (laplace operator)
Falls out that its a positive quality

Seeking to reduce empiral coding rate

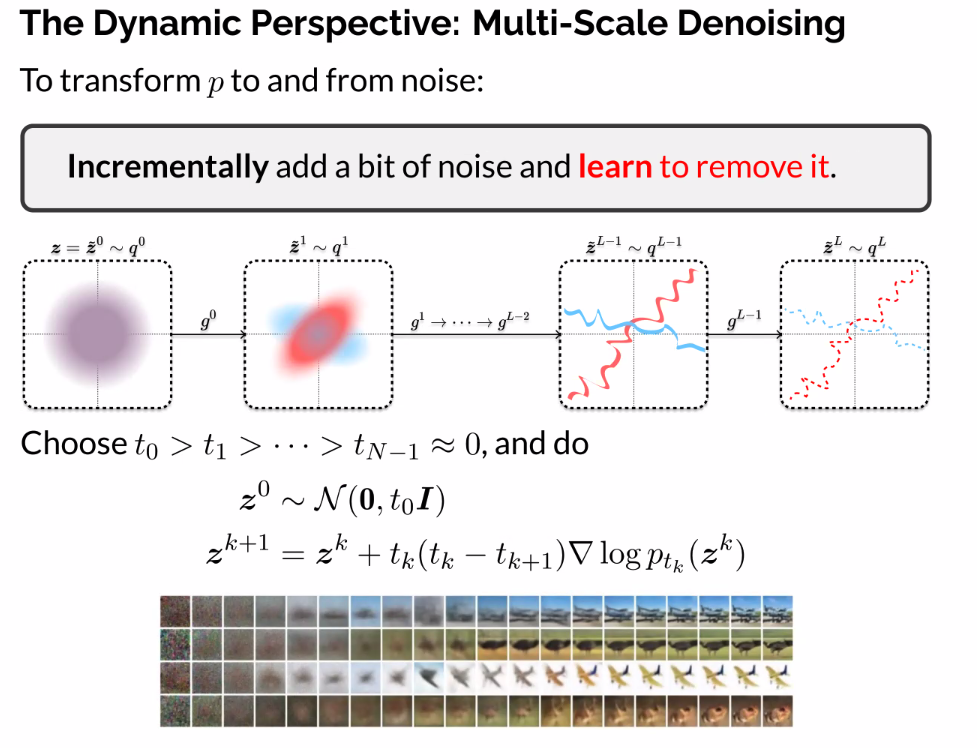
Dynamic Perspective: Multi-Scale Denoising

Add a little noise so that we learn to remove
Keep increasing it, until our model completely understands the underlying data
Noisy manifold?
Depending on how sophisticated the manifold is (corners/cusps), a smooth manifold intuition still implies, just like the circle.
- John’s group investigates this, the strucutre/completeness of the manifold after noising?

A lot of these models are closed so hard to see, but many confirmed diffusion models

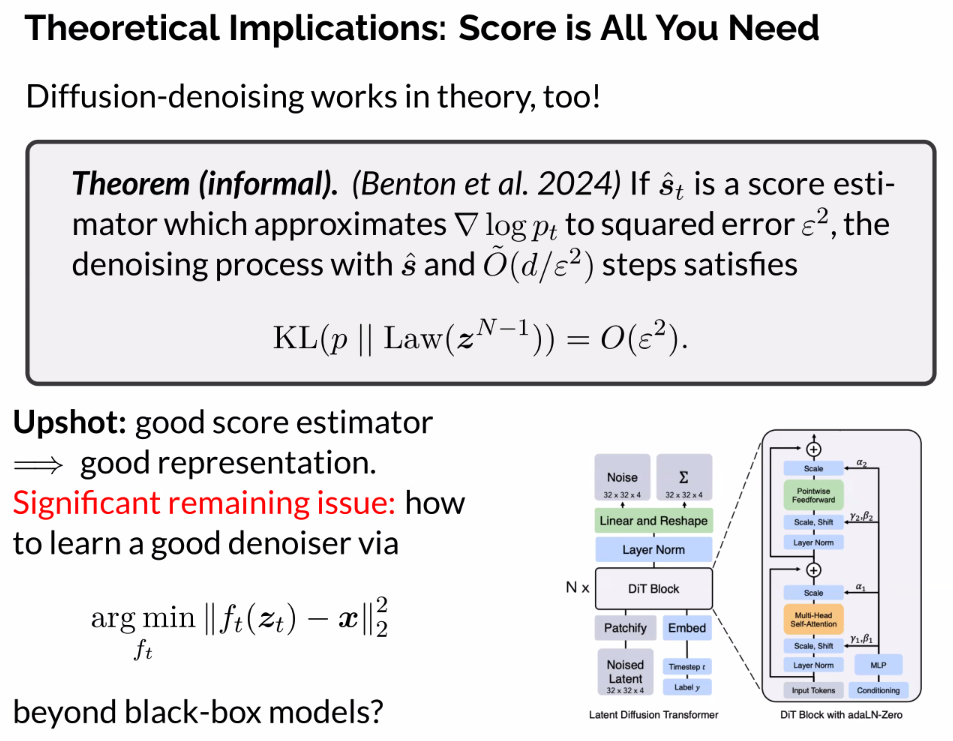
How should you parameterize score functions, represent them in function?
Everything we’ve talked about hinges on a good objective score function

Information Theory

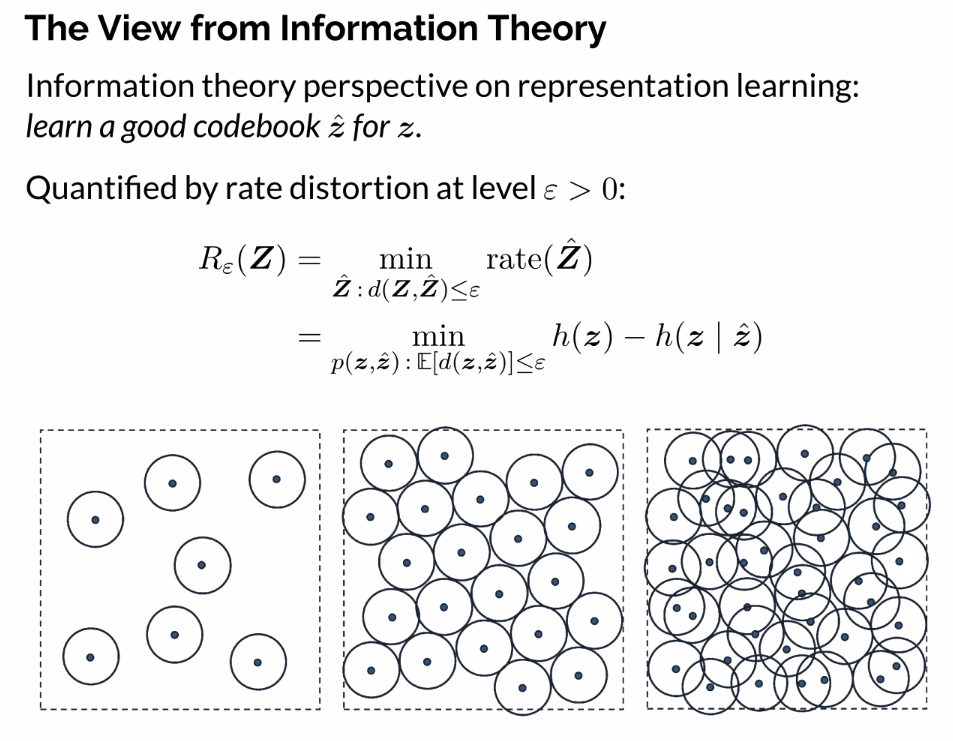
Number of bits needed to represent data, subject to some distortion level
Find a codebook that can represent using short number of bits subject to some small distrotion

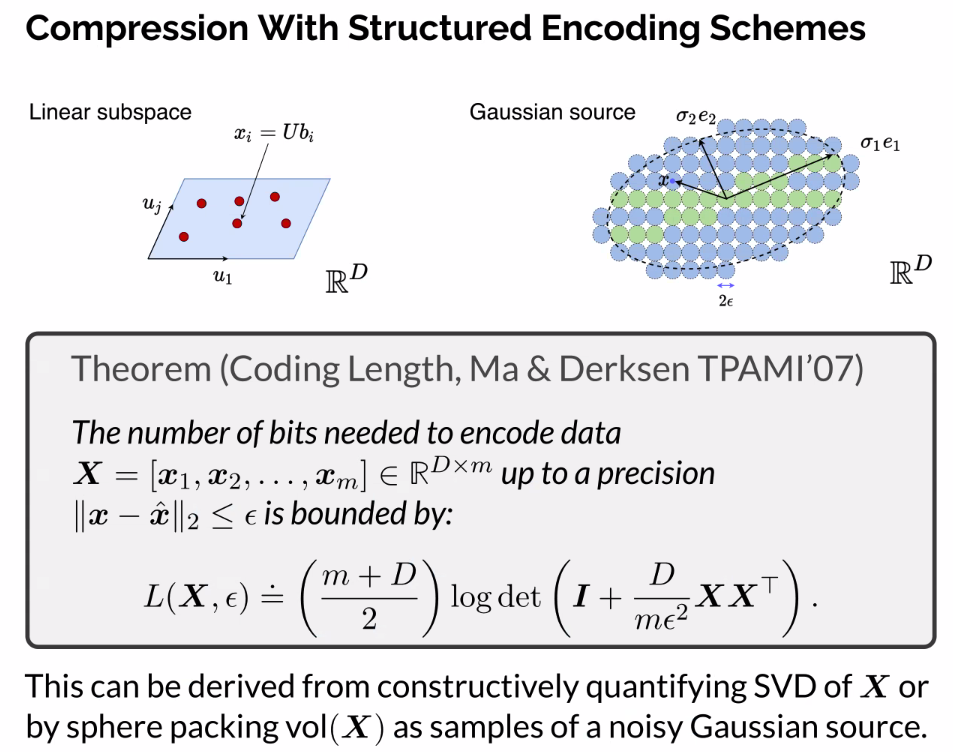
How to compute with a very simple codebook?

If you have data coming from linear structures, it should cost less to structure the data
- If you code the data independently, it should cost you less than coding the data all together
If you were to code the X and Y above all together, you would need to do an ellipsible
If you were to code all together, you could get away with far fewer bits
Seek models for the data such that there’s a big information gain

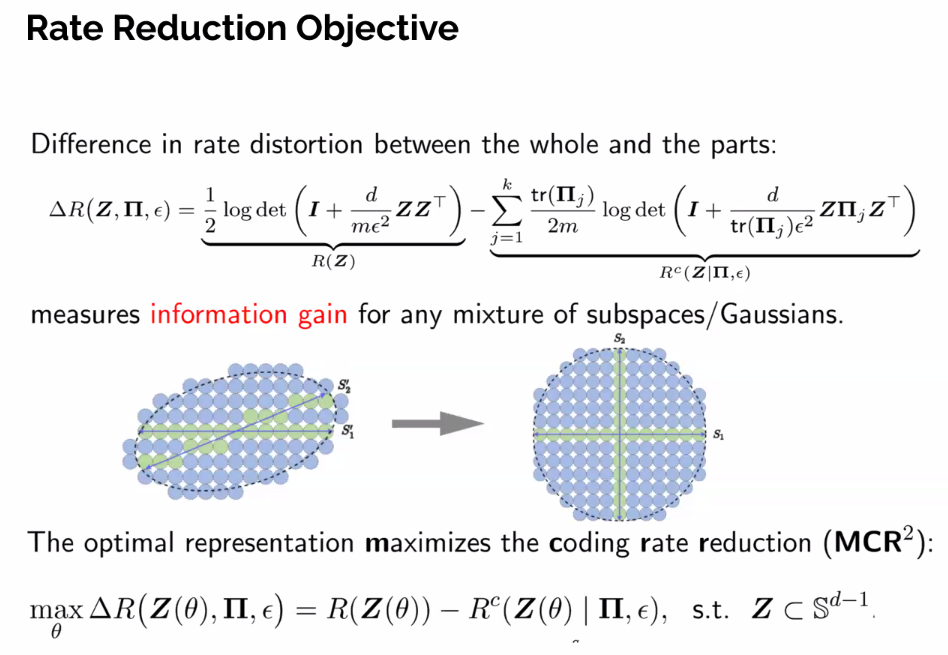
If data comes from mixture of gaussians, you can directly optimize

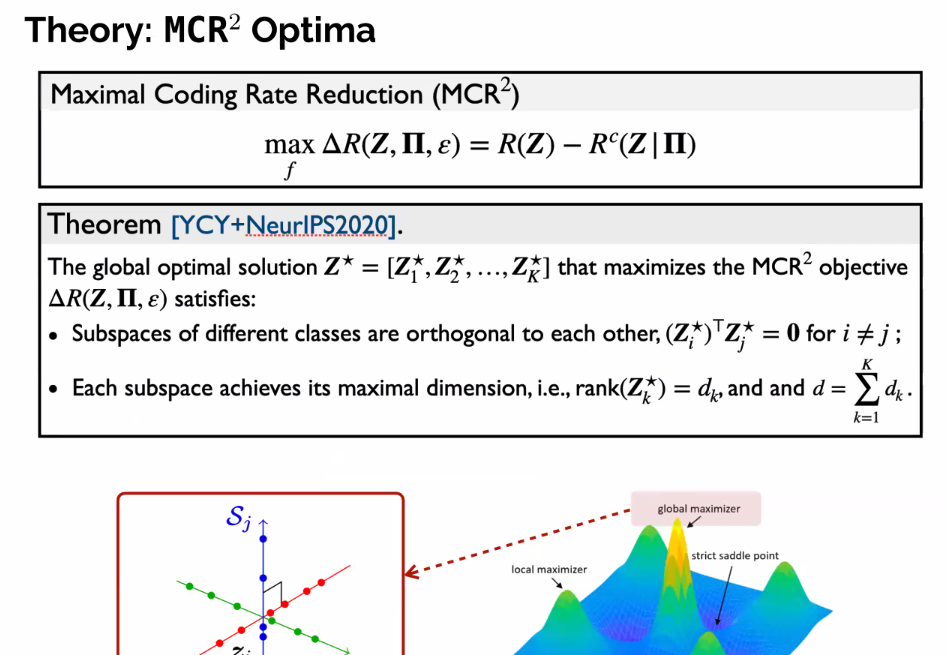
Perfectly optimizing delta r represents to good representations of the data

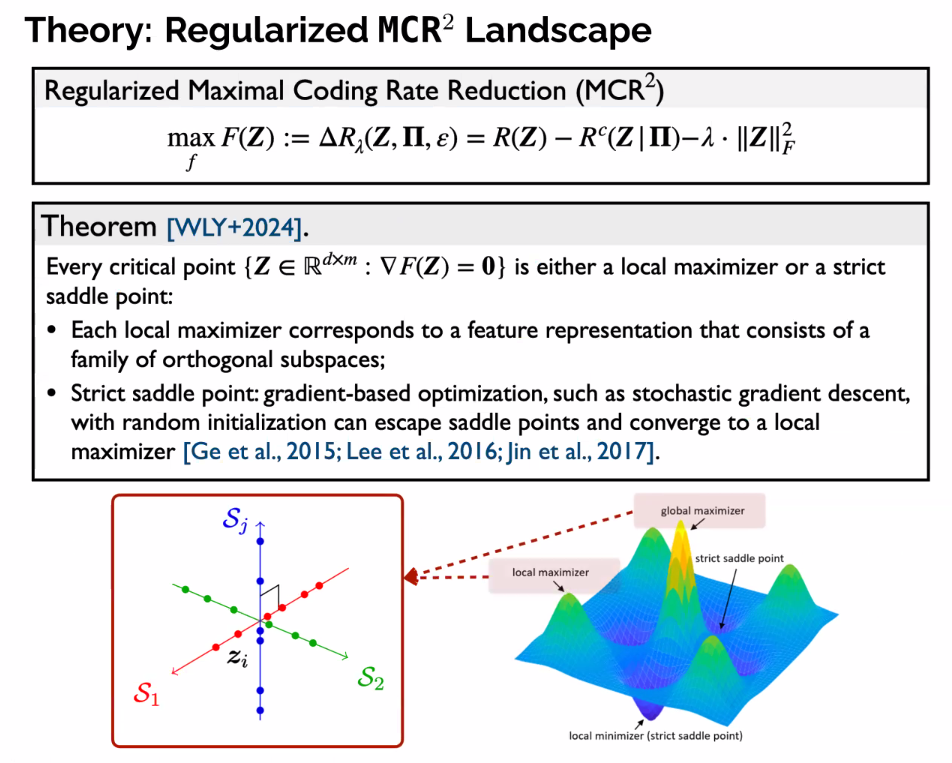
Deep Networks from Optimizing Rate Reduction

Learn representations themselves by slowly optimizing function
Each layer is trying to improve representation/information gain

Unrolled Optimization: From Objectives to Deep Networks

Element wise non linearity
Approach called LISTA, each layer learns its own dictionary

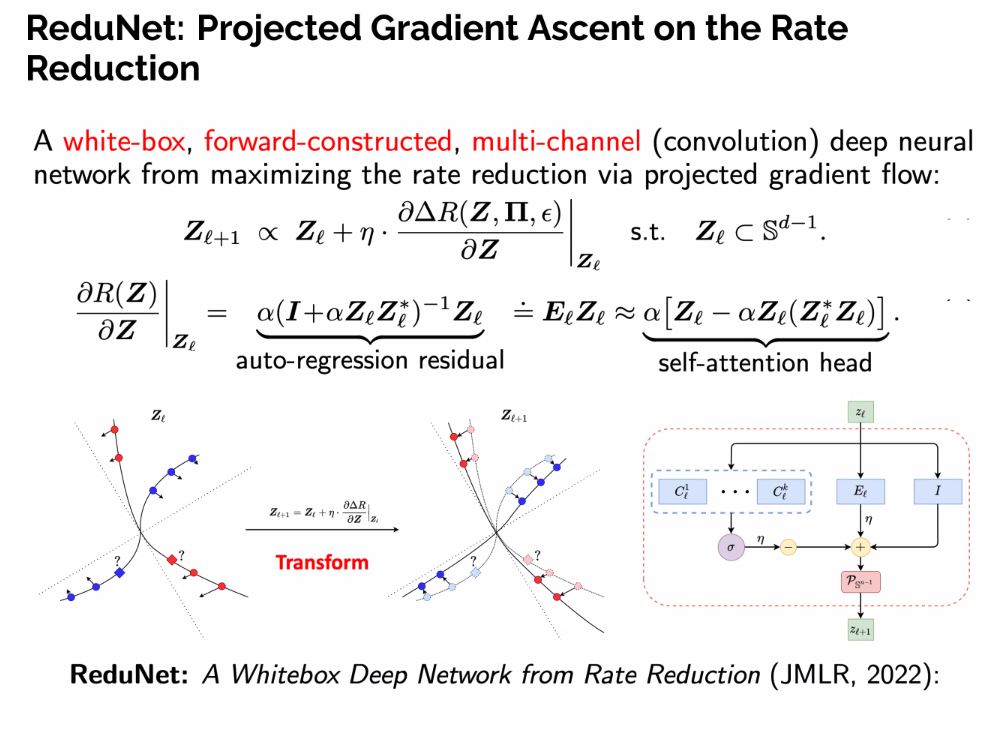
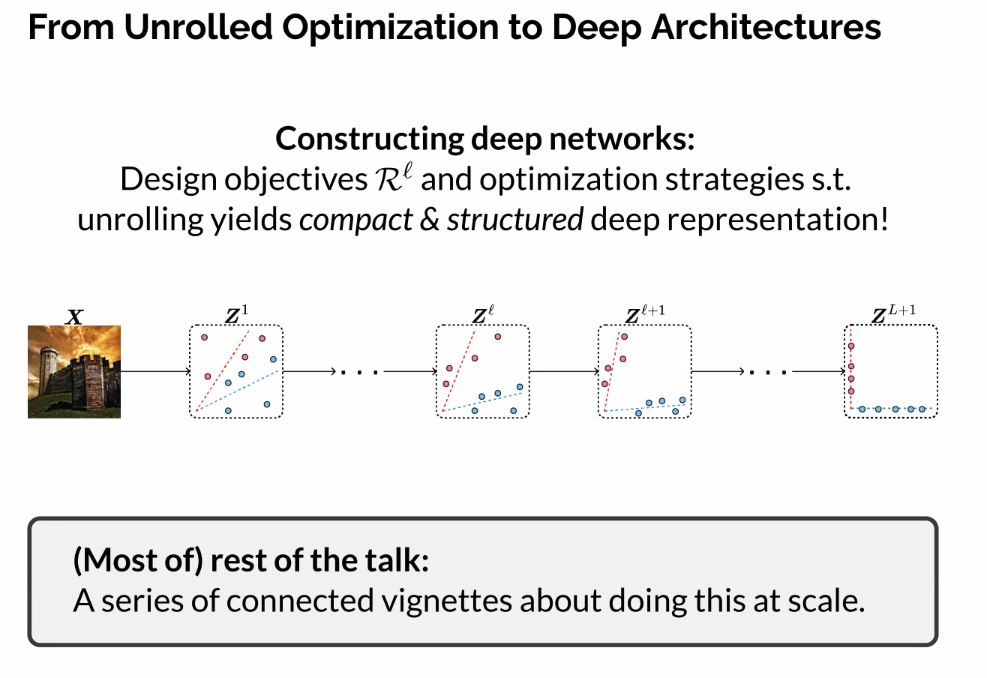
Part Two: Deep Representations via Unrolled Optimizations

Themes:

So far:

Contextualisze representation learning wrt the pursuit of low-dimensional distributions
Elucidate an objective for learning deep representations
Now:
Operationalize this

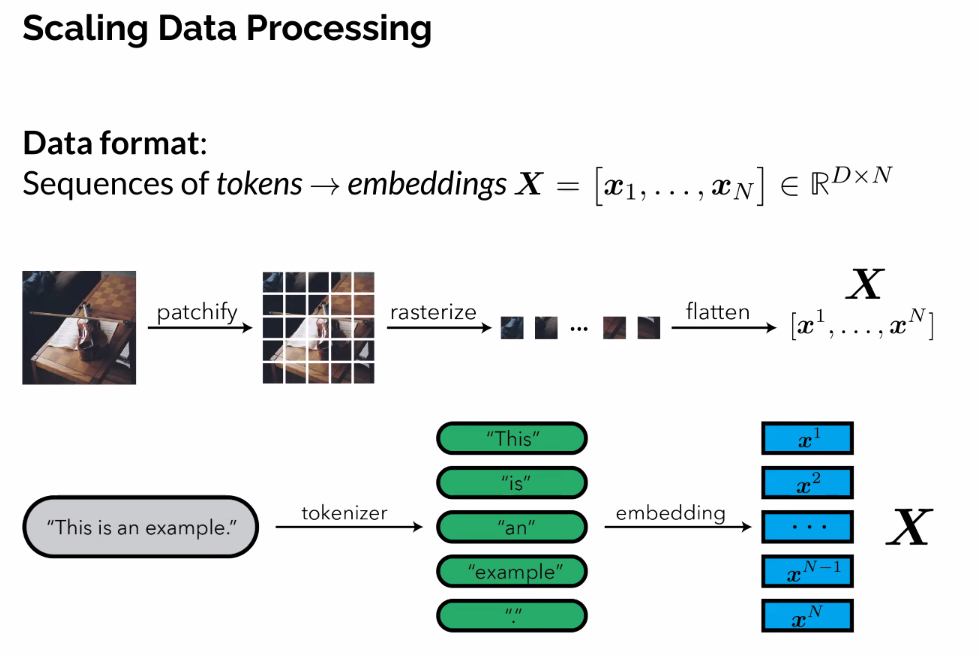
Previously:

Rows correspond to data samples/observations
Now:
Each row represents a token, like in a transformer
The method of reserizing and flattening images into vectors gets a lot of mileage?

High Level of Vision Transformer

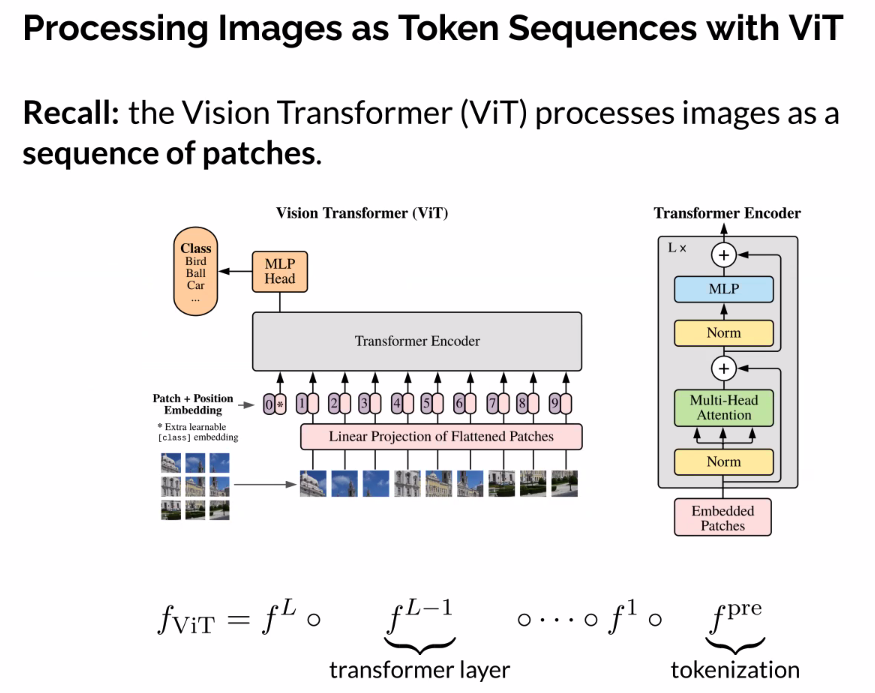
Each layer has a certain strucutre, adaptive to sequence processing

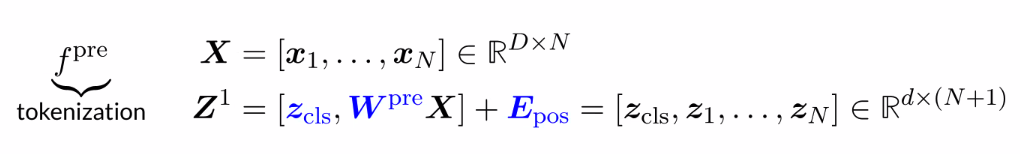
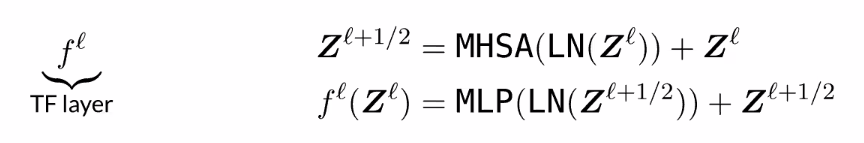
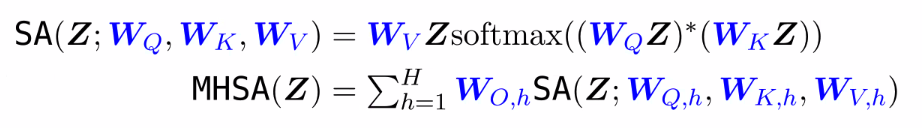
Multiheaded self attention:

Each lay
Calculates corelations between calculated predicted token (seq_len x seq_len)
Normalizes by 1 dimension
Uses normalized scores (projected similrities) to combine with other similarites
“Calculate similarities of the data, and use it to regenerate some of the data”
Multi headed self attention does this in parralel, and uses it in parallel
Usually increases dimension

Stack a bunch of these transformer encoder blocks:

Norm -> Multi head attention -> skip activation and norm -> MLP -> skip and output
Combine them for a transformer

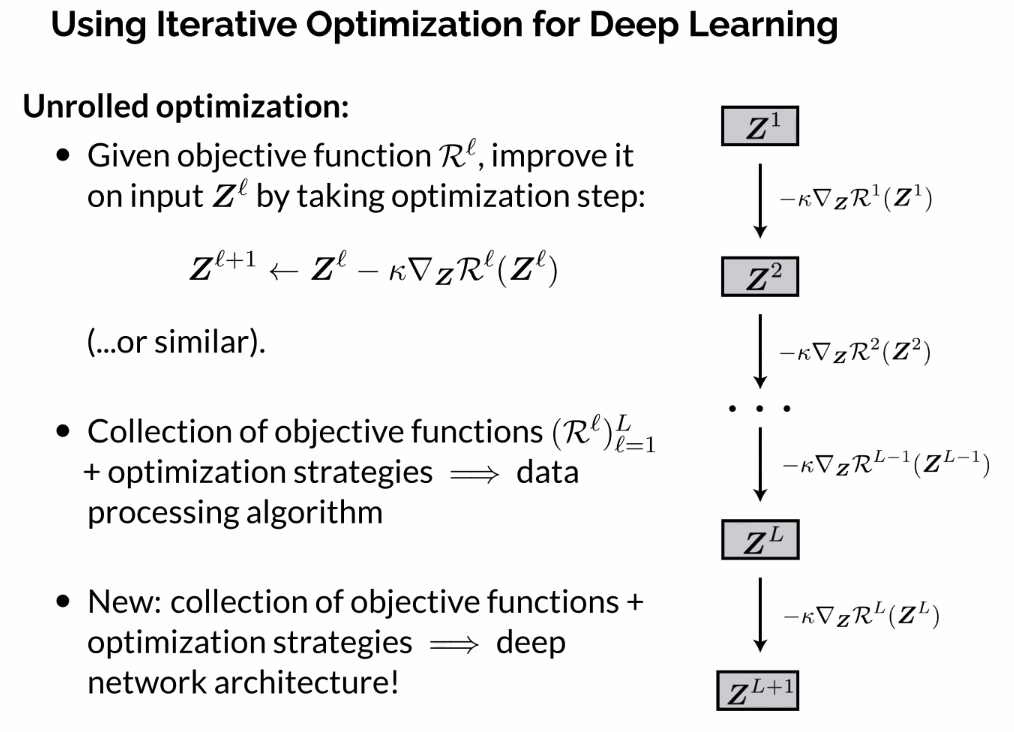
Objective functions that measure representation quality:
- How to choose?

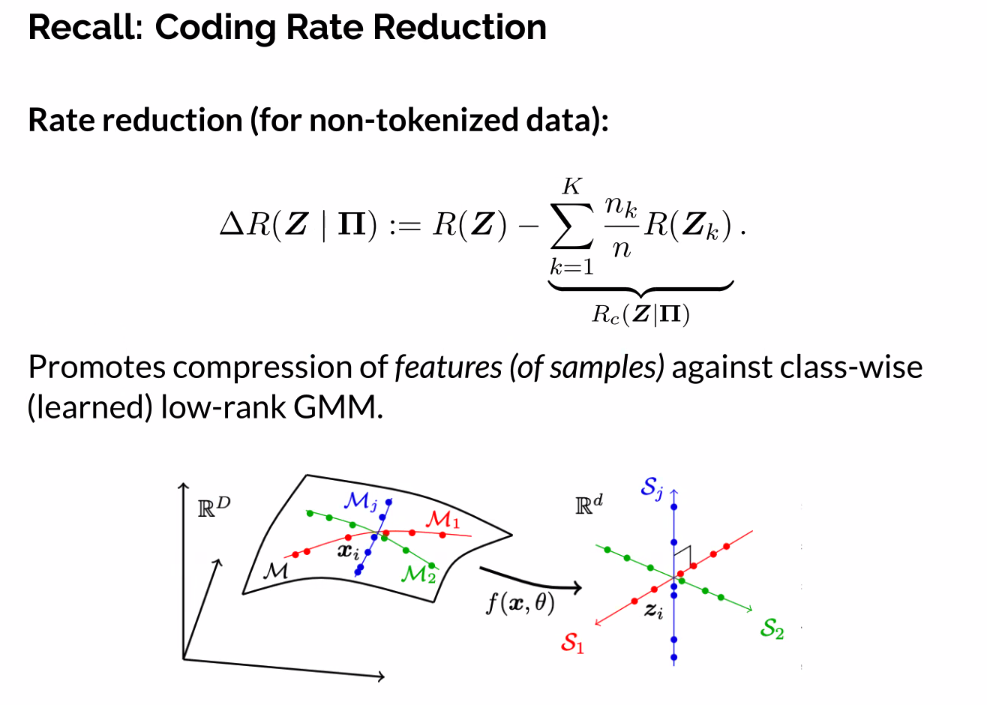
Define information gain objective

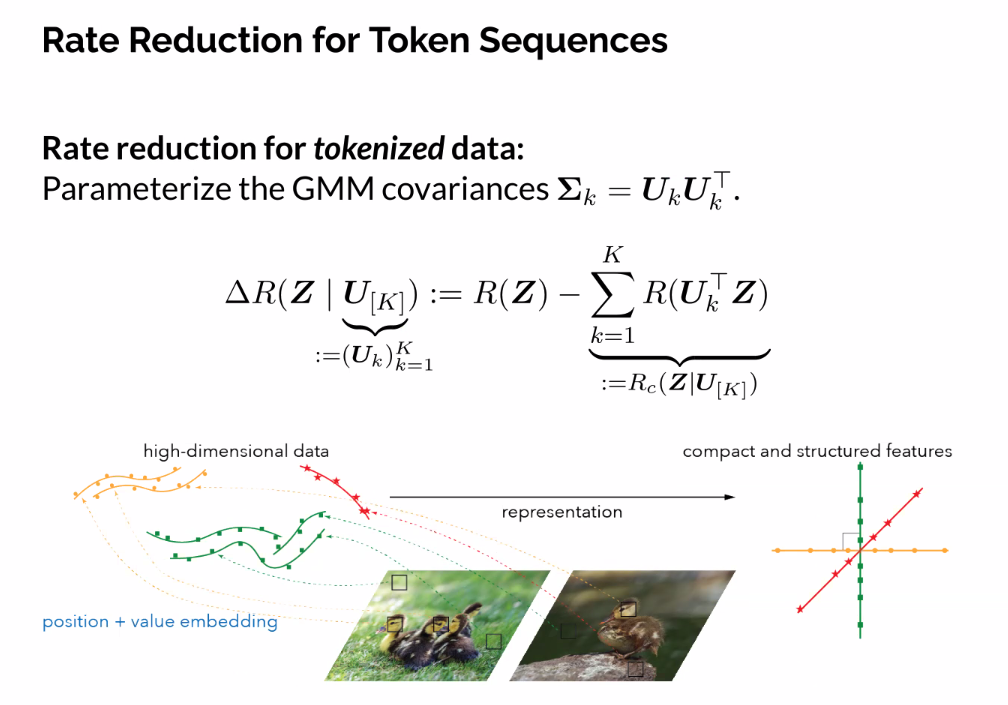
Instead of using hard PI matrix, use soft assignments, learnable by network
- Require that they be orthogonal

The one that’s best with regards to L1 norm is the one that’s sparsest

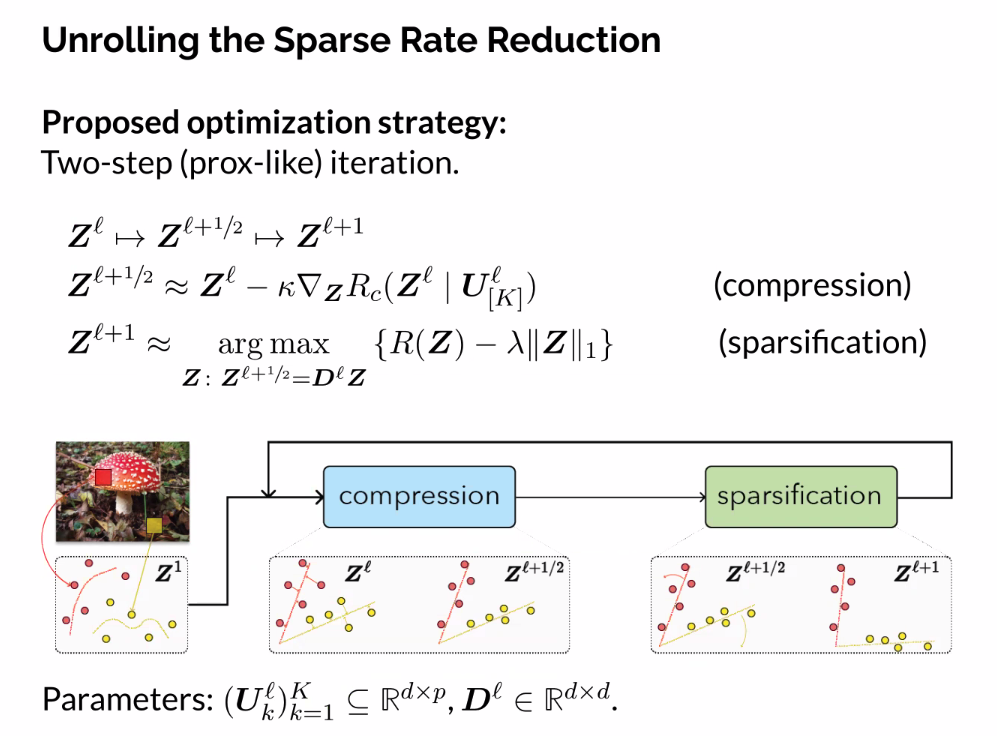
Simple two step optimization of the objective function
- Compression
- Sparsification

Matrix inverse is hard, approximate instead
- How we go from first line to second
In the ideal case that allows us a second approximation jump, we get to our final final
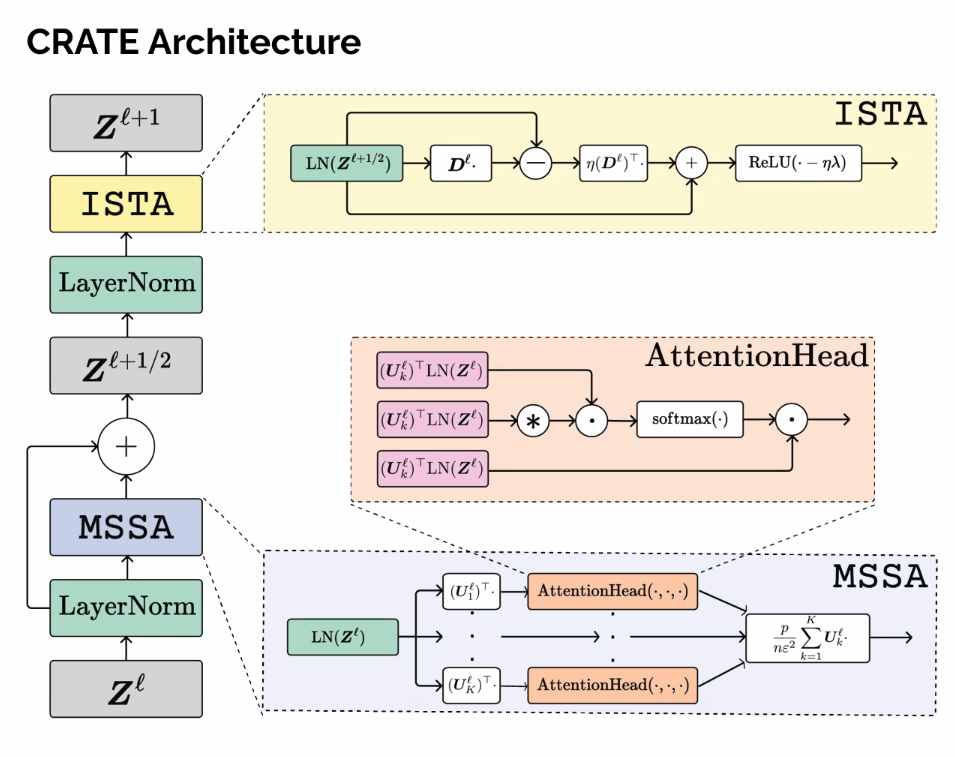
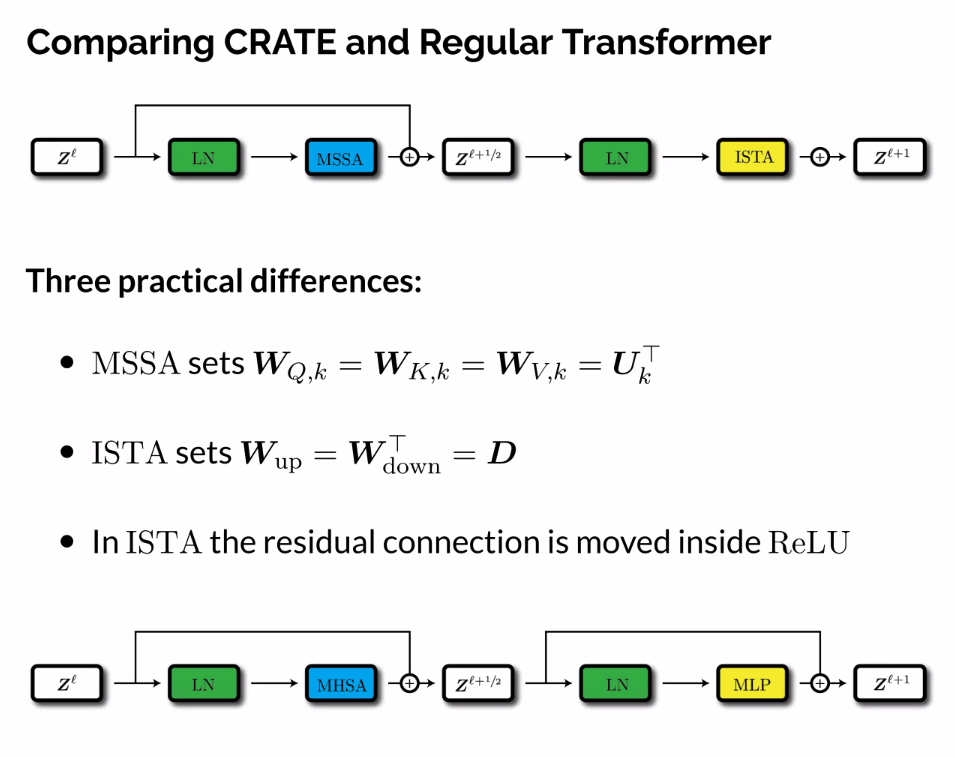
- Add some normalization to the correlation term to improve stability
- Looks much more like the one-headed self attention block
- Normalized porjection between tokens of the set
- Used to …
Key difference is that we get projections, before we had query and key value.
- Each projection is given by the subspace the head is representing
- The operation comes from GD on the compression term and optimizations made for tractability

Sort of to GD on the term

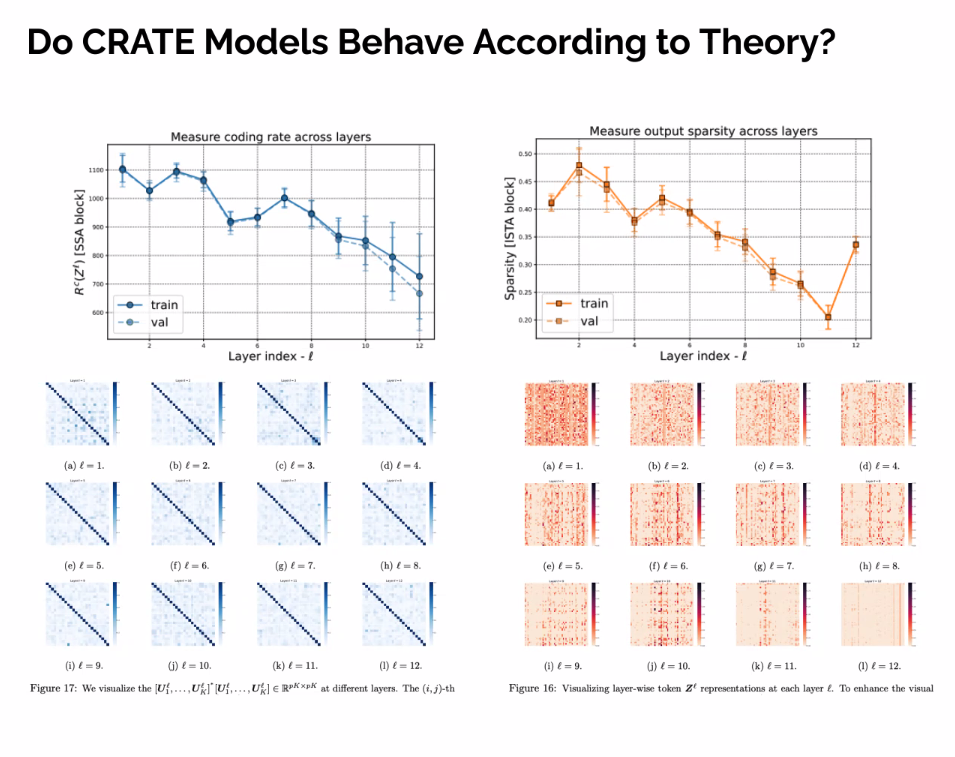
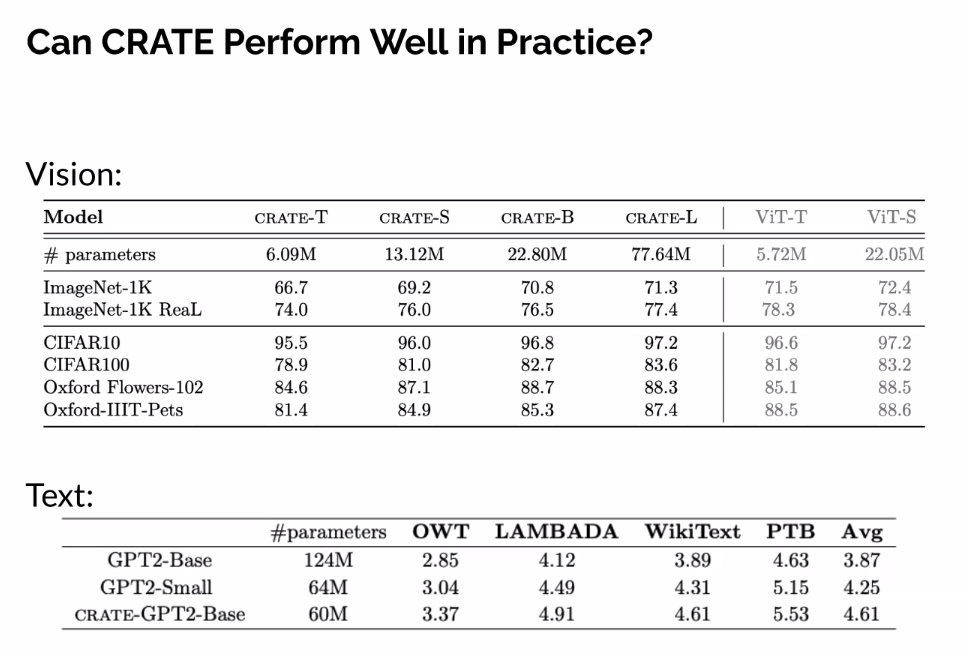
Not incredible, but show viability

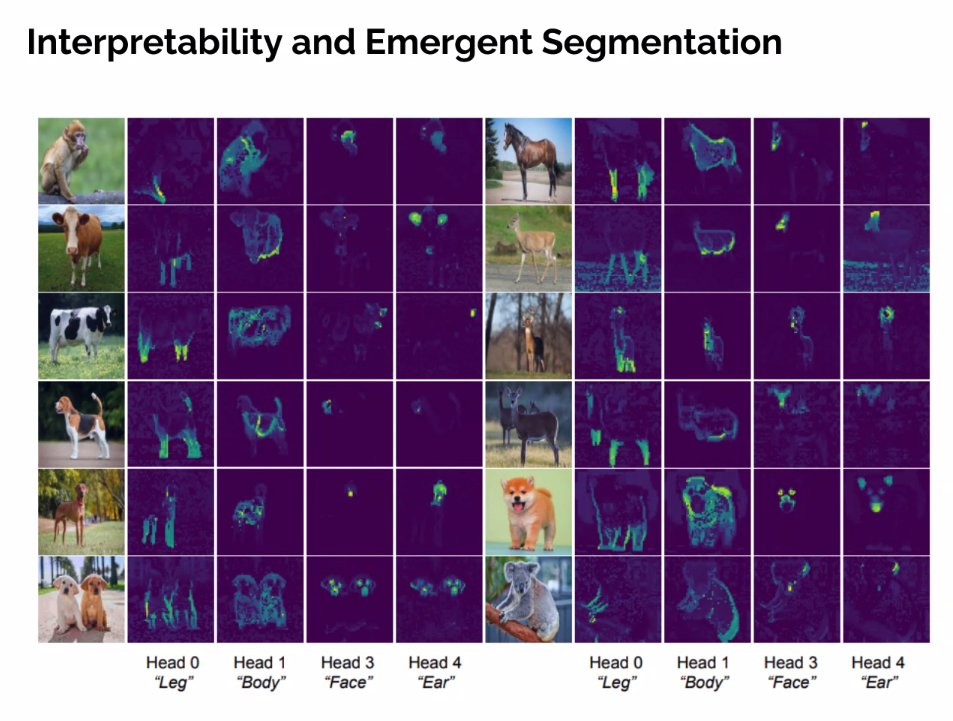
Normal VIT - A large amount of large magnitude outlier token, that make segmentation not accurate to the parts.
- Not doing a good job at this
Confirmed during ablation that is due to the MSSA layers

better emergent sementation, semantic segmentation

Future work?

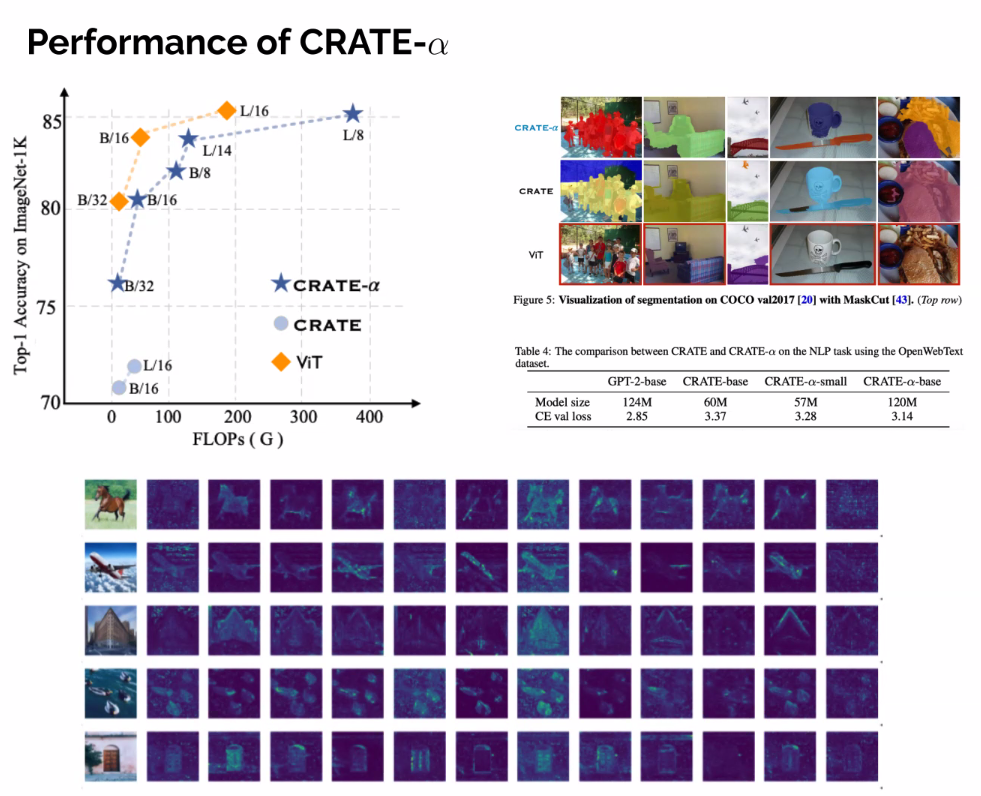
Performance can continued to be scaled through future engineering

Principles for Deep Learning Methodology

On top of suggesting new architecture, rate

Instead of relying on complicated optimization tricks to prevent collapse, switch to objective function of information gain
- Naturally prevents collapse

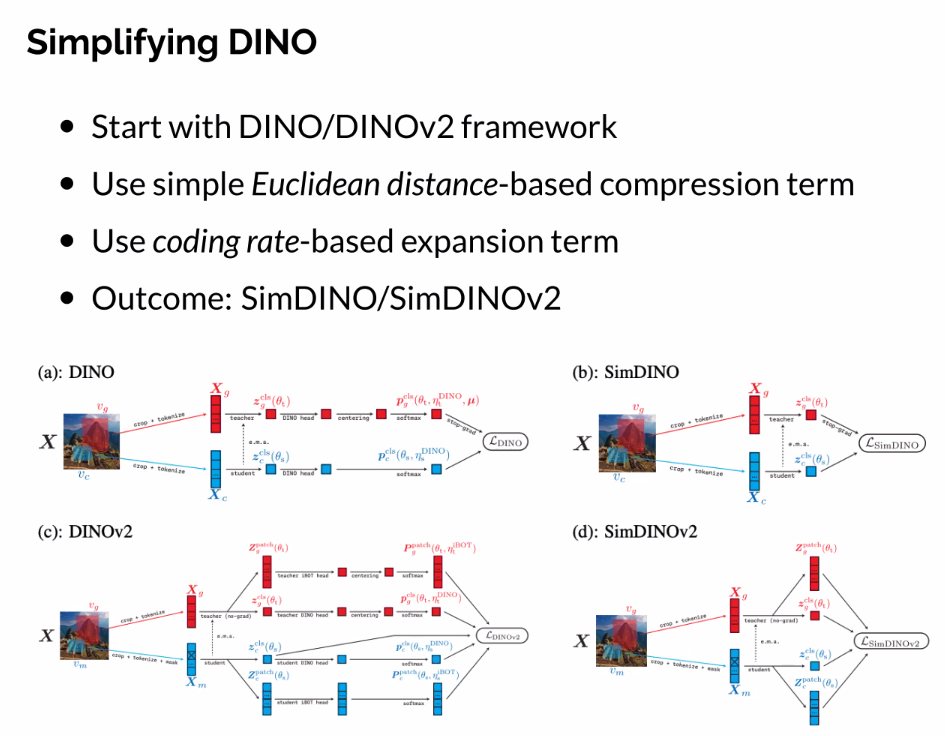
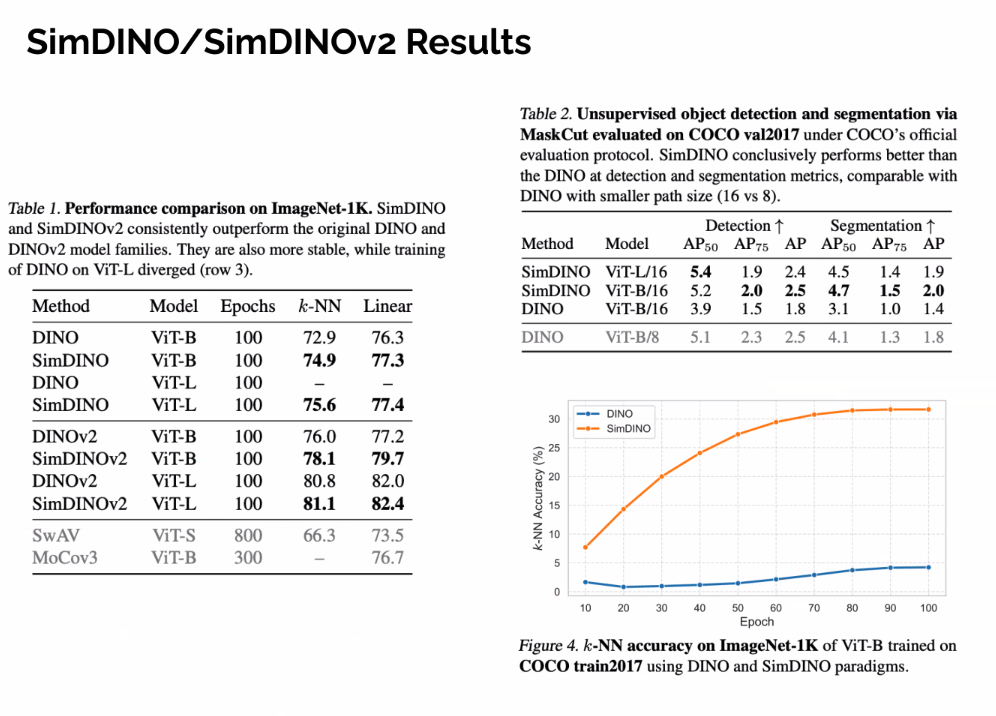
Concluding remarks

Objective for deep representation learning can be operationalized to impact deep architectures/methods.
Resulting architectures sometimes very similar to practice (e.g., CRATE). We can both understand practice and improve on it.
Resulting methods can be significantly better and more stable than previous work (e.g. SimDINO).

The lecture is an overview of an upcoming monograph: Deep Representation Learning of Data Distributions

Filled out the form, hopefully get my hands on it!

🧪 -> Refresh the Info

Did you generally find the overall content understandable or compelling or relevant or not, and why, or which aspects of the reading were most novel or challenging for you and which aspects were most familiar or straightforward?)

Did a specific aspect of the reading raise questions for you or relate to other ideas and findings you’ve encountered, or are there other related issues you wish had been covered?)

🔗 -> Links

Resources

Put useful links here

Connections

Link all related words