📗 -> 04/07/25: Neural Codes
Neural Codes Lecture
Information Theory Primer
🎤 Vocab
❗ Unit and Larger Context
Quick Refresher:
Invasive Recording:
- Intra/Extra Cellular Recording
- ECoG / iEEG
Noninvasive
- fMRI
- Using magnetic field and radio waves to induce a response that measures the relaxation time.
- This gives us info on the BOLD, which is a metabolic process relating to the oxygenation of neurons
- EEG
- Using electrodes to measure scalp voltage
- The scalp voltage is generated from population activity of firing neurons, generating a large dipole
✒️ -> Scratch Notes
Neural Codes
How do neurons exchange information?
- Single neurons vs. population codes
- In a single neuron code it is sufficient to read out the activity of a single neuron for obtaining a desired piece of information.
- In contrast, a population code requires reading out multiple neurons for obtaining the desired information.
- Rate vs. temporal codes
- In a rate code, it is only important how active (firing rate or spikes in an interval) neuron/neurons are. Exact firing time is irrelevant
- In a temporal code, spike times carry information. A single spike could potentially carry information
What are the issues with single neuron rate codes?
- Especially for low firing rates, can be difficult to reliably get an estimate of activity (have to measure for a long time to tell 1 spike/min vs 2 spike/min for instance). Information often needed QUICKLY
- Tuning curves often have a different shape with the strongest response for some optimal stimulus parameter and a falloff to both sides (see slide “Place code vs. value code”). Thus, a particular firing rate is often associated with two possible parameter values.
- More explanation in this part of next lecture: Here
- Activity often modulated by multiple stimulus parameters, not possible to obtain a value from a single neuron
Using population spikes can shorten the time window required for a reliable estimate of firing rate
In principle, the reliability of the firing rate estimate could be constantly improved by adding additional neurons. However, this is only true when all neurons spike independently (no positive correlation).
Variability in neural responses and correlations
-
Responses to repeated presentations of the same stimulus are usually not identical. This tells us there is inherent variability in neural response. This variability is referred to as noise
-
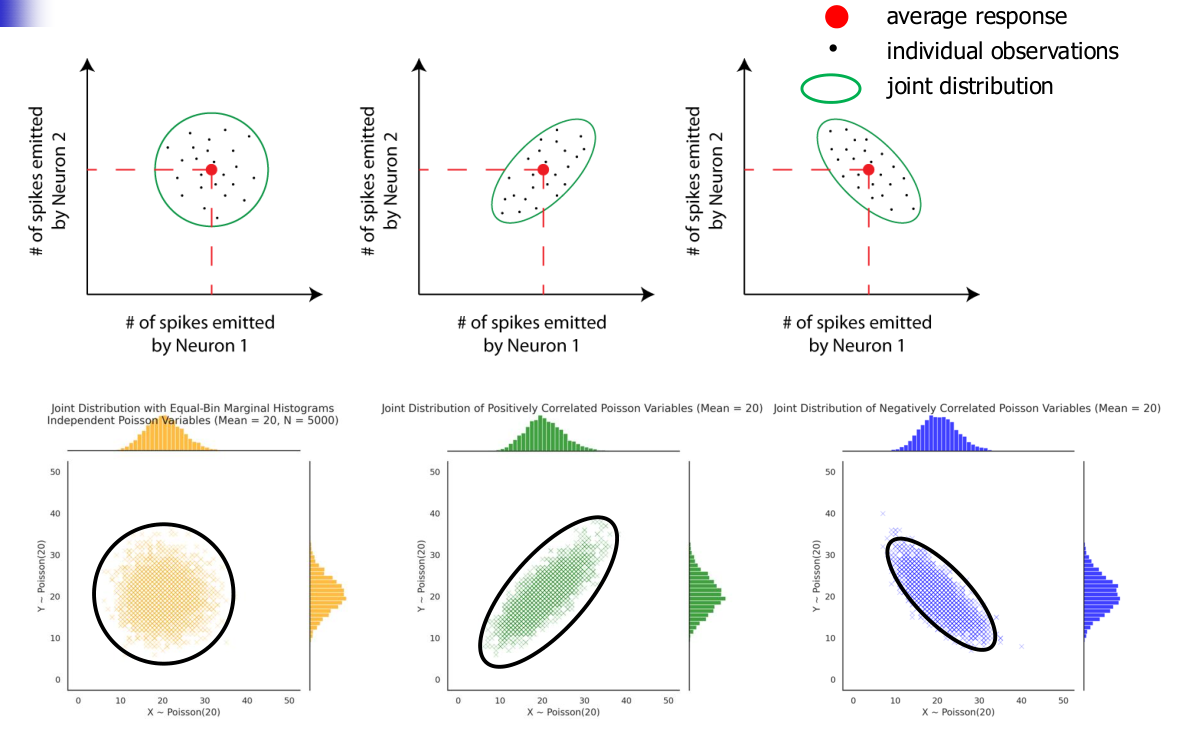
When recording the responses of two different neurons to repeated presentations of the same stimulus simultaneously, both responses will vary across trials. If these variations are (statistically) independent of each other, one says that there is no “noise correlation” between the responses of both neurons
-
If they are not independent, then we will have a noise correlation, which can be either positive or negative.
- Positive: When one neuron had more spikes, the other was more likely to respond with more spikes (than average)
- Negative: When one neuron had more spikes, the other was more likely to respond with a smaller than average number of spikes
-
The width of the joint distribution is also important. The radius for each direction (x/y axis) tells us the number of noise variability for each neuron. ‘Thinner’ radius tells us there is lower variability in the noise
-
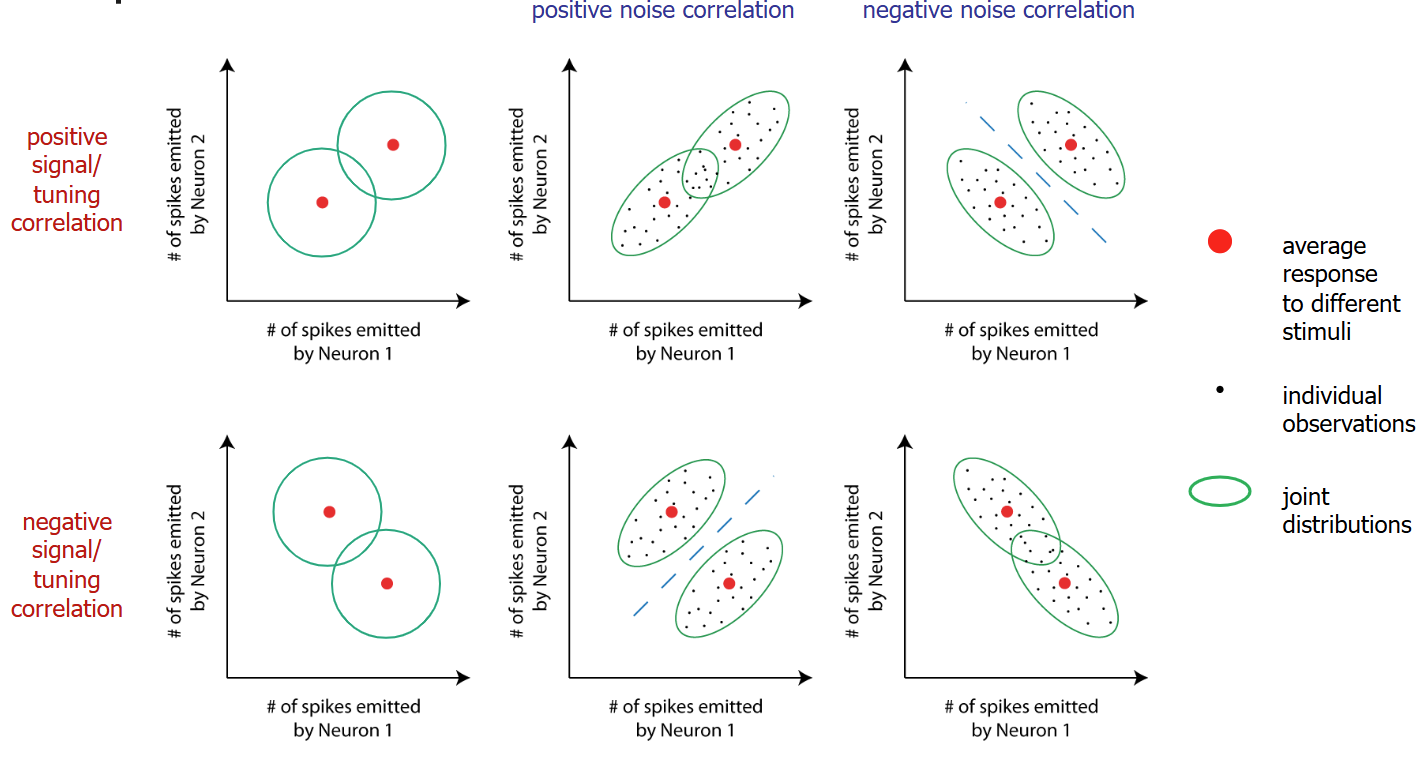
On top of that, we have signal correlation or tuning correlation, which captures how changes in the stimulus affect the average responses of two (or multiple) neurons
- Positive signal correlation means that when one neuron increases its firing rate in response to a stimulus change the other one tends to increase its firing as well (see next slide for an illustration). This typically means that the neurons have similar tuning curves.
- Negative signal correlation means that when one neuron increases its firing rate in response to a stimulus change the other one tends to decrease its firing rate (see next slide for an illustration). This typically means that the neurons have quite different tuning curves.
-
The combination of signal correlation and noise correlation has consequences for how well neural responses to different stimuli can be discriminated (see next slide for an illustration).
-
This is complicated because there’s multiple stimuli. In the previous noise correlation slide, there was only one center/distribution and the noise correlation the source of variance
-
In this new slide, the signal correlation and multiple stimuli is also a factor. We have variation due to signal correlation and noise correlation
Computing noise correlation:
- No Noise:
- Positive Noise:
- Negative Noise:
is the variation is the correlation coefficient
Information Theory (I don’t understand this)
We have a c: correlation coefficient
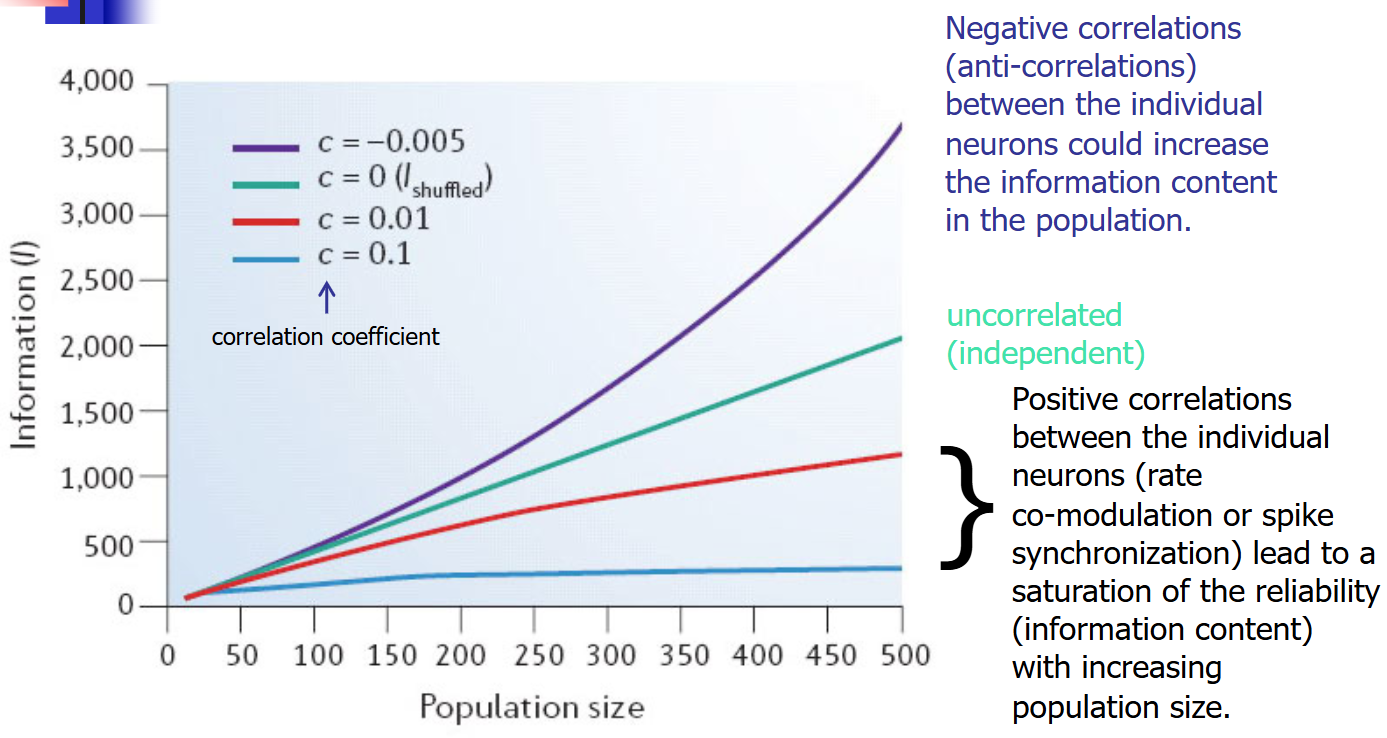
- I understand information saturation, but…
- Still don’t have a strong grasp of what schemes could increase the information content.
Entropy: Cannot be smaller than 0 and it cannot exceed
- The minimum entropy (0) is observed when only a single value has non-zero probability
- The maximum entropy is observed when the distribution is uniform (all values have the same probability).
Mutual Information (how much info X provides about Y and vice versa)
🧪 -> Refresh the Info
Did you generally find the overall content understandable or compelling or relevant or not, and why, or which aspects of the reading were most novel or challenging for you and which aspects were most familiar or straightforward?)
Did a specific aspect of the reading raise questions for you or relate to other ideas and findings you’ve encountered, or are there other related issues you wish had been covered?)
🔗 -> Links
Resources
- Put useful links here
Connections
- Link all related words