📗 -> 04/09/25: NPB163-L4
🎤 Vocab
❗ Unit and Larger Context
Review from last lecture:
- Noise correlation and signal correlation
Information Theory
- Entropy: A variable that represents the uncertainty of another variable or variables
- Entropy is minimized when outcomes are guaranteed (p=0 or p=1) and maximized when outcomes are most unpredictable (which happens when all outcomes are uniform, p=0.5)
Mutual Information:
- Intuitively, its the entropy explained?
moving on…
✒️ -> Scratch Notes
Place code vs. Value Code
Populations of neurons with different tuning curves
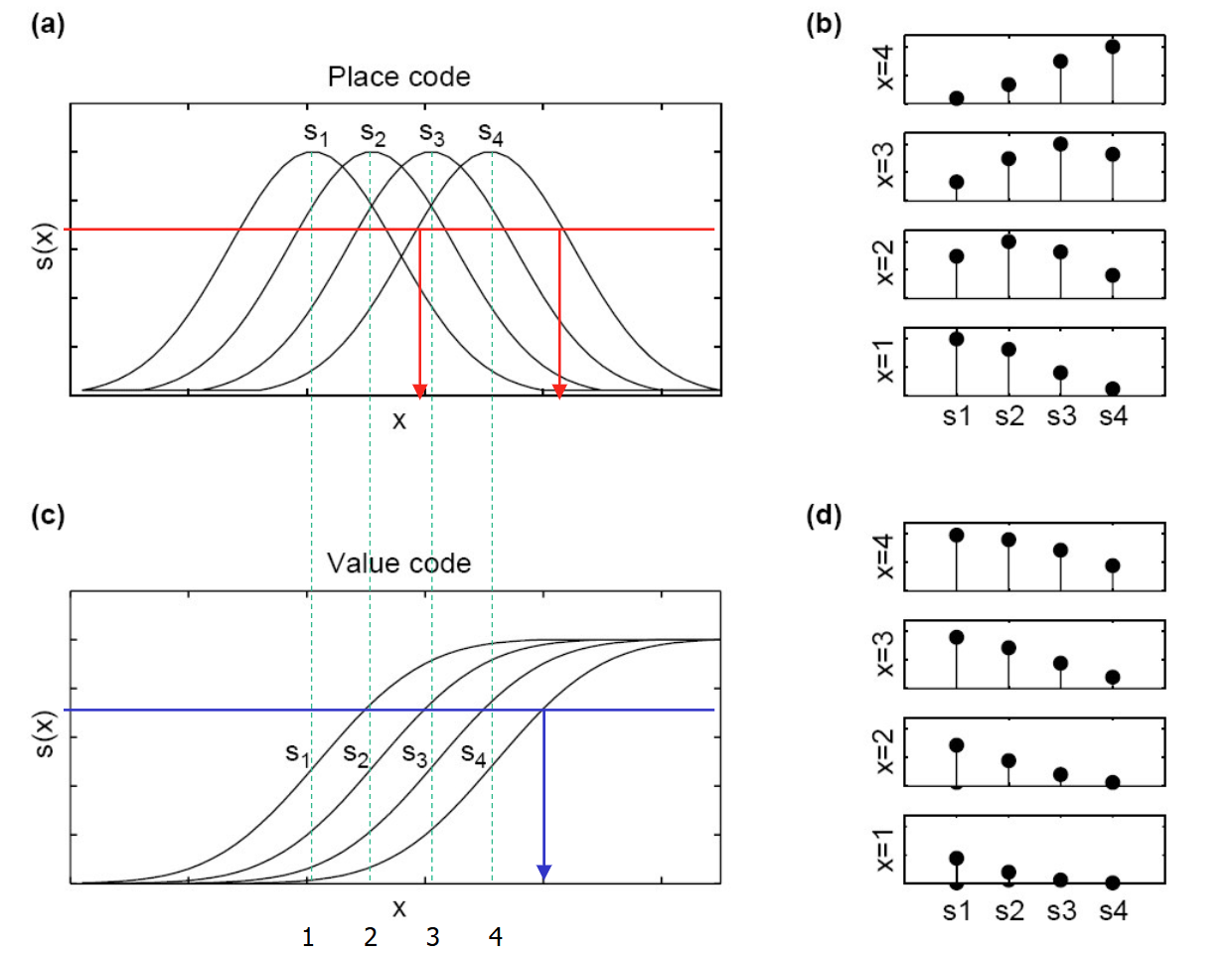
- For a place code, one neuron is not sufficient for telling what the stimulus is (associated with multiple parameter values). Need multiple neurons to be able to tell the true parameter, attribute it to the one producing the HIGHEST activity
- “Associated with multiple parameter values” means the function is not “one-to-one” (like x^2 is not one-to-one), and there is ambiguity at the true parameter producing it
- For a value code, one neuron is sufficient. However, accumulating them in a population activity can increase the range (particularly for low activity inputs, accumulating them), and reduce noise given noise is not correlated
Single Neuron Timing Code
Simplified example (not necessarily accurate)
Neurons in the bat auditory cortex tend to respond to the incoming echo of a vocalization with a single spike. The spike time reflects the time of the echo.
What are the problems with this scheme?
- Spike time has to be interpreted with respect to some reference time
- With bats, they have an internal reference of when they vocalized
- What can be done when there is a priori no internal reference? – Making use of other neurons in the population might help: Temporal population codes
Temporal Population Code
Idea: Generate an internal reference from the population response using coincidence detection
Population average:
Using the population onset as internal reference on average increased the first-spike latency information
What do spike times mean for rate coded neurons?
Exact spike times are the consequence of a random spike generation process and do not carry any relevant information
- Successful models of spike generation using follow a Poisson Process
- Poisson process is a model that predicts time from one occurance to another, predicting that time between follows a exponential distribution. Memoryless between spikes.
The spike generator is usually assumed to be a Poisson process. This means that the number of spikes that are emitted in a particular time interval T follow a Poisson distribution with mean r·T (r = firing rate). One of the properties of a Poisson distribution is that the variance is equal to the mean. The Poisson process is memoryless: when the next event occurs does not depend on the history of events. Radioactive decay is a good example of a Poisson process
However, this doesn’t account for refractory periods. Use a modified Poisson process, with refractory periods.
?
Why wouldn’t uncorrelated signals give the most information? Intuitively, orthogonal signals should give the largest span?
Mutual Information - Effectively information explained?
What any of the temporal pop code slide is saying?
🧪 -> Refresh the Info
Did you generally find the overall content understandable or compelling or relevant or not, and why, or which aspects of the reading were most novel or challenging for you and which aspects were most familiar or straightforward?)
Did a specific aspect of the reading raise questions for you or relate to other ideas and findings you’ve encountered, or are there other related issues you wish had been covered?)
🔗 -> Links
Resources
- Put useful links here
Connections
- Link all related words